Non-cooperative game theory

From HandWiki
Revision as of 23:17, 6 February 2024 by Pchauhan2001 (talk | contribs) (correction)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Type of game involving individual competition

A non-cooperative game is a form of game under the topic of game theory. Non-cooperative games are used in situations where there are competition between the players of the game. In this model, there are no external rules that enforces the cooperation of the players therefore it is typically used to model a competitive environment. This is stated in various accounts most prominent being John Nash's paper.[1]

That being said, there are many arguments to be made regarding this point as with decades of research, it is shown that non-cooperative game models can be used to show cooperation as well and vice versa for cooperative game model being used to show competition.

Some examples of this would be the usage of non-cooperative model in determining the stability and sustainability of cartels and coalitions.[2][3]

Non zero-sum games and zero-sum games are both types of non-cooperative games.[4]

Non-cooperative game theory in academic literature

Referring to the above mentioned John Nash's 1951 article in the journal Annals of Mathematics. Nash Equilibrium, non-cooperative game theory in fact, are often referred to as "non-cooperative equilibrium".[5]

According to Tamer Başar in Lecture Notes on Non-Cooperative Game Theory, a non-cooperative game requires specifying:

  1. the number of players;
  2. the possible actions available to each player, and any constraints that may be imposed on them;
  3. the objective function of each player which he or she attempts to optimise;
  4. any time ordering of the execution of the actions if the players are allowed to act more than once;
  5. any information acquisition that takes place and how the information available to a player at each point in time depends on the past actions of other players, and;
  6. whether there is a player (nature) whose action is the outcome of a probabilistic event with a fixed (known) distribution.[6]
  7. The utility of each player for all action profile.

Assumptions

  1. Perfect recall: each player remembers their decisions and known information.[7]
  2. Self-interest: each player does not consider the effect of actions on the others but only on their own.[7]
  3. Rational: each player is interested to maximise their utility or payoff.[8][9]
  4. Complete information: each player knows the preferences and strategies of the other players.[8]
  5. Each player has the same understanding of how the game is.[8]

Creating a non-cooperative game (basic game)

In order to understand the usage of the non-cooperative game model, we must first understand how to create a non-cooperative game.

The following will provide the requirements to create a basic non-cooperation game to encourage a basic understanding of the model

First, following the above mentioned requirements, we need to know how many players there are. For simplicity in explanation, let the number of players be n. In a 2 or 3 player game, it is still relatively easy to represent the game in a matrix. However, as they number of player increases, it becomes significantly hard and more time consuming to do so. As such we represent it in a form of mathematical equations.

Therefore the Player set would look like this {1,....., n}.

Secondly, We need to determine the possible actions that can be taken by each of the players. For simplicity in explanation, let the set of actions of a player be denoted as X

Therefore the action of player the player set will look like this {X1,....., Xn}.

Lastly, we will have to determine the utility of the player for each action profile. For this criteria, there is no fixed methodology as the utility of each player is determined by the perceived benefits of the outcome. However in theory, we generally assign a value to a player's utility so that we are able to determine each player's rational decision and preferred outcome. This is different from expected utility which is covered when solving the game[1][6][10]

You can refer to the list of common examples below to see how these steps creates a non-competitive game.

Analysis

Non-cooperative games are generally analysed through the non-cooperative game theory framework, which attempts to predict players' individual strategies and payoffs and in order to find the Nash equilibria.[11][12] This framework often requires a detailed knowledge in the possible actions and the levels of information of each player.[13] It is opposed to cooperative game theory, which focuses on predicting which groups of players ("coalitions") will form, the joint actions that these groups will take, and the resulting collective payoffs that arise. Cooperative game theory does not analyse the strategic bargaining that occurs within each coalition and affects the distribution of the collective payoff between the members. Further in contrast to cooperative game theory, it is assumed that players involved have prior knowledge of their game in which they are involved, due to built in commitments.[14]

Non-cooperative game theory provides a low-level approach as it models all the procedural details of the game, whereas cooperative game theory only describes the structure, strategies and payoffs of coalitions. Therefore, cooperative game theory is referred to as coalitional, and non-cooperative game theory is procedural.[13] Non-cooperative game theory is in this sense more inclusive than cooperative game theory.

It is also more general, as cooperative games can be analysed using the terms of non-cooperative game theory where arbitration is available to enforce an agreement, that agreement falls outside the scope of non-cooperative theory: but it may be possible to state sufficient assumptions to encompass all the possible strategies players may adopt, in relation to arbitration. This will bring the agreement within the scope of non-cooperative theory. Alternatively, it may be possible to describe the arbitrator as a party to the agreement and model the relevant processes and payoffs suitably.

Accordingly, it would be desirable to have all games expressed under a non-cooperative framework. But in many instances insufficient information is available to accurately model the formal procedures available to the players during the strategic bargaining process; or the resulting model would be of too high complexity to offer a practical tool in the real world. In such cases, cooperative game theory provides a simplified approach that allows analysis of the game at large without having to make any assumption about bargaining powers.

Additionally, we must also look at the limitations that the non-cooperative model may have. We can have a clearer picture when looking at the list of assumptions stated above. As already mentioned, there are many scenarios where perfect symmetry of information is not possible which therefore results in the decision making process to be flawed.[15]

Secondly, the assumption of self-interest and rationality could be argued. Arguments are made that being rational can result in the assumption of self-interest being invalidated and vice versa. One such example could be the reduction in profits and revenue in attempts to drive out competitors for a higher market share. This thus does not follow both of the assumptions as the player is concerned with the downfall of their opponent more than the maximisation of their profits. There is the argument to be made that although mathematically sound and feasible, it is not necessarily the best method of looking at real life economical problems that are more complex in nature.[15]

Examples

Strategic games are also a form of non-cooperative game theory, where only the available strategies and combinations of options are listed to produce outcomes.

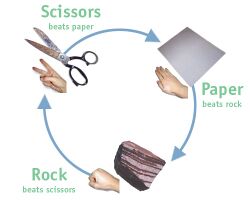
Rock-paper-scissors

Main page: Rock paper scissors
Rock paper scissors.jpg

The simple example is the game of rock-paper-scissors. In the game of rock-paper-scissors, there is no cooperative option between the two players available: if Player 1 decides to play "rock", it is in Player 2's interest to play "paper"'; if Player 2 chooses to play "paper", it is in Player 1's interest to play "scissors"; and if Player 1 plays "scissors", Player 2 will, in their own interests, play "rock". The preferences of the players is cyclical, with no cooperative outcome being reached. This fails the transitive preference property.

Two children steal sweets

Suppose a shopkeeper catches two children for stealing sweets. The two children spoke separately with the shop owner in the shop office. In this case, the children have only two options: to remain silent (neither child admits it) or to say that their peers stole the sweets. If one child admits to stealing the sweets and the other does not, the child who admits will receive a warning, and the other child will be punished for four weeks. If both children admit to stealing the sweets, they will both receive a two-week punishment. If they both deny it, then both children will be punished for three weeks. One child must rely on the idea of another child to avoid minor punishment. The connection between them is that game theory generally looks at how individuals or groups make choices that will affect other parties.

Two children for steal sweets
Child A/ Child B Recognition Non-recognition
Recognition -2, -2 0, -4
Non-recognition -4, 0 -3, -3

The two children's first thought must have been their interests, but this would have led to the most extended punishment for both. The best option for them is for them to both admit and punish for a fortnight. Thus, this is the Nash equilibrium, also called the non-cooperative equilibrium.

Prisoner's Dilemma

Main page: Philosophy:Prisoner's dilemma
A standard form Prisoner's Dilemma game.

The Prisoner's Dilemma game is another well-known example of a non-cooperative game. The game involves two players, or defendants, who are kept in separate rooms and thus are unable to communicate. Players must decide, by themselves in isolation, whether to cooperate with the other player or to betray them and confess to law authorities. As shown in the diagram, both players will receive a higher payoff in the form of a lower jail sentence if they both remain silent. If both confess, they receive a lower payoff in the form of a higher jail sentence. If one player confesses and the other remain silent and cooperates, the confessor will receive a higher payoff, while the silent player will receive a lower payoff than if both players cooperated with each other.

The Nash equilibrium therefore lies where players both betray each other, in the players protecting oneself from being punished more.

The battle of the sexes game

The game involves two players, boy and girl, deciding either going to a football game or going to an opera for their date, which respectively represent boy's and girl's preferred activity (i.e. boy prefers football game and girl prefers opera).[16] This example is a two-person non-cooperative non-zero sum (TNNC) game with opposite payoffs or conflicting preferences.[16] Because there are two Nash equilibria, this case is a pure coordination problem with no possibility of refinement or selection.[8] Thus, the two players will try to maximise their own payoff or to sacrifice for the other and yet these strategy without coordination will lead to two outcomes with even worse payoffs for both if they have disagreement on what to do on their date.

The battle of the sexes game
Boy/ Girl Football Opera
Football (2, 1) (-1, -1)
Opera (-1, -1) (1, 2)

Matching pennies game

This game is a two-person zero-sum game. In order to play this game, both players will each need to be given a fair two-sided penny. To start the game, both player will each choose to either flip their penny to heads or tails. This action is to be done in secrecy and there should be no attempt at investigating the choice of the other player. After both players have confirmed their decisions, they will simultaneously reveal their choices. This concludes the actions taken by the players to determine the outcome.[10]

The win condition for this game is different for both players. For simplicity in explanation, lets denote the players as Player 1 and Player 2. In order for Player 1 to win, the faces of the pennies must match (This means they must both be heads or tails). In order for Player 2 to win, the faces of the pennies must be different (This means that they must be in a combination of heads and tails).[10]

The payoff/prize of this game is receiving the loser's penny in addition to your own.

Therefore the payoff matrix will look like this:

Player1 \ Player 2 Heads Tails
Heads 1, -1 -1, 1
Tails -1, 1 1, -1

Looking at this matrix, we can conclude a few basic observations.[10]

  1. For all scenarios, there will be a loser and a winner.
  2. This is a zero sum game where the pay out to the winner is equal to the loss of the loser.
  3. There is no Pure Strategy Nash Equilibrium.

For a more detailed and comprehensive treatment, refer to the main article.

The difference between cooperative and non-cooperative game theory

There is a distinction between cooperative game theory and non-cooperative game theory, which follows Nash's statement: “This (cooperative game) theory is based on an analysis of the interrelationships of the various coalitions which can be formed by the players of the game. Our (non-cooperative game) theory, in contradistinction, is based on the absence of coalitions in that it is assumed that each participant acts independently, without collaboration or communication with any of the others.”[17]

Non-cooperative game theory models different situations in which agents are unable to reach a resolution to a conflict that enforces some action on one another.[18][7] This form of game theory pays close attention to the individuals involved and their rational decision making.[13] There are winners and losers in each case, and yet agents may end up in Pareto-inferior outcomes, where every agent is worse off and there is an potential outcome for every agent to be better off.[19] Agents will have the ability to predict what their opponents will do. Cooperative game theory models situations in which a binding agreement is possible. In other words, the cooperative game theory implies that agents cooperate to achieve a common goal and they are not necessarily referred to as a team because the correct term is the coalition. Each agent has its skills or contributions that provide strength to the coalition.[20]

Further, it has been supposed that non-cooperative game theory is purported to analyse the effect of independent decisions on society as a whole.[21] In comparison, cooperative game theory focuses only on the effects of participants in a certain coalition, when the coalition attempts to improve the collective welfare.[21]

Many results or solutions proposed by the agents involved in Game Theory are important in understanding the rivalry between these agents under a set of conditions that are strategic.[18]

Solutions

Solutions in non-cooperative games are similar to all other games in game theory, but without the ones involved binding agreements enforced by the external authority. The solutions are normally based on the concept of Nash equilibrium, and these solutions are reached by using methods listed in Solution concept. Most solutions used in non-cooperative game are refinements developed from Nash equilibrium, including the minimax mixed-strategy proved by John von Neumann.[19][9][22]

See also

References

  1. ↑ 1.0 1.1 Nash, John (1951). "Non-Cooperative Games". Annals of Mathematics 54 (2): 286–295. doi:10.2307/1969529. ISSN 0003-486X. https://www.jstor.org/stable/1969529. 
  2. ↑ Palsule-Desai, Omkar D. (2015-03-01). "Complete Versus Partial Collusion in Competing Coalitions". International Game Theory Review 17 (1): 1540006. doi:10.1142/S021919891540006X. ISSN 0219-1989. https://www.worldscientific.com/doi/10.1142/S021919891540006X. 
  3. ↑ (in en-US) The Endogenous Formation of Economic Coalitions. Edward Elgar Publishing. 2003-06-26. doi:10.4337/9781781009888. ISBN 978-1-78100-988-8. https://www.elgaronline.com/display/184376265X.xml. 
  4. ↑ Ibrahim, Khalid (4 October 2021). "Anti-Jamming Game to Combat Intelligent Jamming for Cognitive Radio Networks". IEEE Access 9: 137941–137956. doi:10.1109/ACCESS.2021.3117563. 
  5. ↑ "A Brief Introduction to NON-COOPERATIVE GAME THEORY". 2010-06-10. http://www.ewp.rpi.edu/hartford/~stoddj/BE/IntroGameT.htm. 
  6. ↑ 6.0 6.1 Başar, Tamer (26 January 2010). "Lecture Notes on Non-Cooperative Game Theory". Hamilton Institute and CTVR in Trinity College, Dublin, Ireland. https://hassan.kharazi.net/blog/wp-content/uploads/2012/12/T10-H7-Lecture-Notes-on-Non-Cooperative-Game-Theory-Tamer-Ba%C2%B8sar.pdf. 
  7. ↑ 7.0 7.1 7.2 Fujiwara-Greve, Takako (2015). "Non-Cooperative Game Theory". Monographs in Mathematical Economics 1. doi:10.1007/978-4-431-55645-9. ISBN 978-4-431-55644-2. ISSN 2364-8279. http://dx.doi.org/10.1007/978-4-431-55645-9. 
  8. ↑ 8.0 8.1 8.2 8.3 Aguirre, Iñaki. "Notes on Non-Cooperative Game Theory-Microeconomic Theory IV". http://www.ehu.eus/iaguirre/MicroIVEnglish/NotesGames2009.pdf. 
  9. ↑ 9.0 9.1 Von Neumann, John (2007). Theory of games and economic behavior. Princeton Univ. Pr. ISBN 978-0-691-13061-3. OCLC 1081636887. http://worldcat.org/oclc/1081636887. 
  10. ↑ 10.0 10.1 10.2 10.3 Takako, Fujiwara-Greve (23 October 2016) (in en). Non-Cooperative Game Theory. Monographs in Mathematical Economics. 1 (1st ed.). Springer Tokyo. doi:10.1007/978-4-431-55645-9. ISBN 978-4-431-56415-7. https://link.springer.com/book/10.1007/978-4-431-55645-9. 
  11. ↑ Chandrasekaran, R.. "Cooperative Game Theory". http://www.utdallas.edu/~chandra/documents/6311/coopgames.pdf. 
  12. ↑ Brandenburger, Adam. "Cooperative Game Theory: Characteristic Functions, Allocations, Marginal Contribution". http://www.uib.cat/depart/deeweb/pdi/hdeelbm0/arxius_decisions_and_games/cooperative_game_theory-brandenburger.pdf. 
  13. ↑ 13.0 13.1 13.2 Chatain, Olivier (2018). "Cooperative and Non-cooperative Game Theory". in Augier, Mie; Teece, David J.. London: Palgrave Macmillan UK. pp. 345–346. doi:10.1057/978-1-137-00772-8_468. ISBN 978-0-230-53721-7. 
  14. ↑ van Damme, E (2001). "Game theory: Noncooperative Game". https://www.sciencedirect.com/topics/economics-econometrics-and-finance/noncooperative-game. 
  15. ↑ 15.0 15.1 Michaelides, Panayotis G.; Papadakis, Theodoulos Eleftherios (28 January 2023) (in en). History of Economic Ideas (1st ed.). Palgrave Macmillan Cham. pp. 117–131. doi:10.1007/978-3-031-19697-3. ISBN 978-3-031-19697-3. https://link.springer.com/book/10.1007/978-3-031-19697-3. 
  16. ↑ 16.0 16.1 Biswas, Tapan (1997). Decision-Making under Uncertainty. doi:10.1007/978-1-349-25817-8. ISBN 978-0-333-66261-8. 
  17. ↑ Nash, John (1997-12-31), "3. Non-Cooperative Games. Annals of Mathematics 54 (1951) 286-295.", Classics in Game Theory (Princeton University Press): pp. 14–26, doi:10.1515/9781400829156-008, ISBN 9781400829156, http://dx.doi.org/10.1515/9781400829156-008, retrieved 2022-04-27 
  18. ↑ 18.0 18.1 Aguirre, Inaki (2023-04-24). "Non-Cooperative Game Theory". https://www.ehu.eus/iaguirre/MicroIVEnglish/NotesGames2009.pdf. 
  19. ↑ 19.0 19.1 "Noncooperative Games". https://www.encyclopedia.com/social-sciences/applied-and-social-sciences-magazines/noncooperative-games. 
  20. ↑ Hamidi, Maryam; Liao, Haitao; Szidarovszky, Ferenc (2016-11-16). "Non-cooperative and cooperative game-theoretic models for usage-based lease contracts" (in en). European Journal of Operational Research 255 (1): 163–174. doi:10.1016/j.ejor.2016.04.064. ISSN 0377-2217. 
  21. ↑ 21.0 21.1 (in en-gb) Non-Cooperative Game Theory. Monographs in Mathematical Economics. 1. 2015. doi:10.1007/978-4-431-55645-9. ISBN 978-4-431-55644-2. https://link.springer.com/content/pdf/10.1007/978-4-431-55645-9.pdf. 
  22. ↑ v. Neumann, J. (December 1928). "Zur Theorie der Gesellschaftsspiele". Mathematische Annalen 100 (1): 295–320. doi:10.1007/bf01448847. ISSN 0025-5831. http://dx.doi.org/10.1007/bf01448847. 

External links

it:Teoria dei giochi#Giochi non cooperativi



Retrieved from "https://handwiki.org/wiki/index.php?title=Non-cooperative_game_theory&oldid=3387301"