Biology:Hille equation
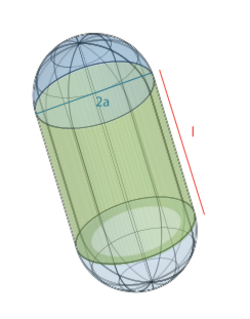
The Hille equation relates the maximum ionic conductance of an ion channel to its length and radius (or diameter), with the commonly used version implicitly takes into account a hemispherical cap.[1] As it is ultimately based on a macroscopic continuum model, it does not take into account molecular interactions, and real conductances are often several times less than the predicted maximal flux.
Assumptions and Derivations
Equation
The Hille equation predicts the following maximum conductance [math]\displaystyle{ g }[/math] for a pore with length [math]\displaystyle{ l }[/math], radius [math]\displaystyle{ a }[/math], in a solvent with resistivity [math]\displaystyle{ \rho }[/math]:
[math]\displaystyle{ \frac{1}{g} = (l+\pi\frac{a}{2}) \times{} \frac{\rho}{\pi{}a^2} }[/math]
Rearranging the terms, the maximal flux based on length [math]\displaystyle{ l }[/math] and diameter [math]\displaystyle{ d }[/math] can be shown to be:
[math]\displaystyle{ \frac{1}{g} = \frac{l\rho}{(\pi{}(\frac{d}{2})^2)} + \frac{\rho}{d} }[/math]
Physical Implications
References
- ↑ Hille, Bertil (2001). Ion channels of excitable membranes'. Sunderland, MA: Sinauer Associates. ISBN 978-0-87893-321-1.
 |