Convex lattice polytope

			Error creating thumbnail: File with dimensions greater than 12.5 MP
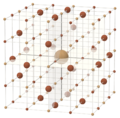
Cube	Cuboctahedron	Octahedron	Truncated octahedron
(±1, ±1, ±1)	(0, ±1, ±1)	(0, 0, ±1)	(0, ±1, ±2)
Four convex lattice polytopes in three dimensions

A convex lattice polytope (also called Z-polyhedron or Z-polytope) is a geometric object playing an important role in discrete geometry and combinatorial commutative algebra. It is a polytope in a Euclidean space Rⁿ which is a convex hull of finitely many points in the integer lattice Zⁿ ⊂ Rⁿ. Such objects are prominently featured in the theory of toric varieties, where they correspond to polarized projective toric varieties.

Examples

• An n-dimensional simplex Δ in Rⁿ⁺¹ is the convex hull of n+1 points that do not lie on a single affine hyperplane. The simplex is a convex lattice polytope if (and only if) the vertices have integral coordinates. The corresponding toric variety is the n-dimensional projective space Pⁿ.
• The unit cube in Rⁿ, whose vertices are the 2ⁿ points all of whose coordinates are 0 or 1, is a convex lattice polytope. The corresponding toric variety is the Segre embedding of the n-fold product of the projective line P¹.
• In the special case of two-dimensional convex lattice polytopes in R², they are also known as convex lattice polygons.
• In algebraic geometry, an important instance of lattice polytopes called the Newton polytopes are the convex hulls of the set [math]\displaystyle{ A }[/math] which consists of all the exponent vectors appearing in a collection of monomials. For example, consider the polynomial of the form [math]\displaystyle{ axy+bx^2+cy^5+d }[/math] with [math]\displaystyle{ a,b,c,d \neq 0 }[/math] has a lattice equal to the triangle

[math]\displaystyle{ {\rm conv}(\{(1,1),(2,0),(0,5),(0,0)\}). }[/math]

See also

• Normal polytope
• Pick's theorem
• Ehrhart polynomial
• Integer points in convex polyhedra

References

• Ezra Miller, Bernd Sturmfels, Combinatorial commutative algebra. Graduate Texts in Mathematics, 227. Springer-Verlag, New York, 2005. xiv+417 pp. ISBN:0-387-22356-8