Inverse Pythagorean theorem

Short description: Relation between the side lengths and altitude of a right triangle

Comparison of the inverse Pythagorean theorem with the Pythagorean theorem using the smallest positive integer inverse-Pythagorean triple in the table below.

Base Pytha- gorean triple	AC	BC	CD		AB
(3,  4,  5)	20 =  4× 5	15 =  3× 5	12 =  3× 4		25 =  52
(5, 12, 13)	156 = 12×13	65 =  5×13	60 =  5×12		169 = 132
(8, 15, 17)	255 = 15×17	136 =  8×17	120 =  8×15		289 = 172
(7, 24, 25)	600 = 24×25	175 =  7×25	168 =  7×24		625 = 252
(20, 21, 29)	609 = 21×29	580 = 20×29	420 = 20×21		841 = 292
All positive integer primitive inverse-Pythagorean triples having up to three digits, with the hypotenuse for comparison

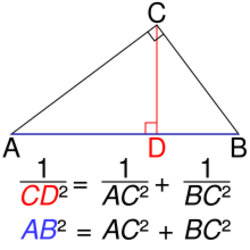
In geometry, the inverse Pythagorean theorem (also known as the reciprocal Pythagorean theorem or the upside down Pythagorean theorem) is as follows:

Let A, B be the endpoints of the hypotenuse of a right triangle △ABC. Let D be the foot of a perpendicular dropped from C, the vertex of the right angle, to the hypotenuse. Then

$\frac{1}{C{D}^2}=\frac{1}{A{C}^2}+\frac{1}{B{C}^2}.$

This theorem should not be confused with proposition 48 in book 1 of Euclid's Elements, the converse of the Pythagorean theorem, which states that if the square on one side of a triangle is equal to the sum of the squares on the other two sides then the other two sides contain a right angle.

Proof

The area of triangle △ABC can be expressed in terms of either AC and BC, or AB and CD:

$\begin{array}{rl}\frac{1}{2}AC\cdot BC& =\frac{1}{2}AB\cdot CD\\ (AC\cdot BC{)}^2& =(AB\cdot CD{)}^2\\ \frac{1}{C{D}^2}& =\frac{A{B}^2}{A{C}^2\cdot B{C}^2}\end{array}$

given CD > 0, AC > 0 and BC > 0.

Using the Pythagorean theorem,

$\begin{array}{rl}\frac{1}{C{D}^2}& =\frac{B{C}^2+A{C}^2}{A{C}^2\cdot B{C}^2}\\ & =\frac{B{C}^2}{A{C}^2\cdot B{C}^2}+\frac{A{C}^2}{A{C}^2\cdot B{C}^2}\\ \therefore \frac{1}{C{D}^2}& =\frac{1}{A{C}^2}+\frac{1}{B{C}^2}\end{array}$

as above.

Special case of the cruciform curve

The cruciform curve or cross curve is a quartic plane curve given by the equation

$x^2{y}^2-b^2{x}^2-a^2{y}^2=0$

where the two parameters determining the shape of the curve, a and b are each CD.

Substituting x with AC and y with BC gives

$\begin{array}{rl}A{C}^{2}B{C}^2-C{D}^{2}A{C}^2-C{D}^{2}B{C}^2& =0\\ A{C}^{2}B{C}^2& =C{D}^{2}B{C}^2+C{D}^{2}A{C}^2\\ \frac{1}{C{D}^2}& =\frac{B{C}^2}{A{C}^2\cdot B{C}^2}+\frac{A{C}^2}{A{C}^2\cdot B{C}^2}\\ \therefore \frac{1}{C{D}^2}& =\frac{1}{A{C}^2}+\frac{1}{B{C}^2}\end{array}$

Inverse-Pythagorean triples can be generated using integer parameters t and u as follows.

$\begin{array}{rl}AC& =(t^2+u^2)(t^2-u^2)\\ BC& =2tu(t^2+u^2)\\ CD& =2tu(t^2-u^2)\end{array}$

Application

If two identical lamps are placed at A and B, the theorem and the inverse-square law imply that the light intensity at C is the same as when a single lamp is placed at D.

See also

• Geometric mean theorem – Theorem about right triangles
• Pythagorean theorem – Relation between sides of a right triangle