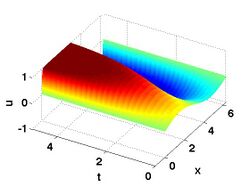
Allen–Cahn equation
The Allen–Cahn equation (after John W. Cahn and Sam Allen) is a reaction–diffusion equation of mathematical physics which describes the process of phase separation in multi-component alloy systems, including order-disorder transitions.
The equation describes the time evolution of a scalar-valued state variable [math]\displaystyle{ \eta }[/math] on a domain [math]\displaystyle{ \Omega }[/math] during a time interval [math]\displaystyle{ \mathcal{T} }[/math], and is given by:[1][2]
- [math]\displaystyle{ {{\partial \eta}\over{\partial t}}=M_\eta[\operatorname{div}(\varepsilon^{2}_{\eta}\nabla\,\eta)-f'(\eta)]\quad \text{on } \Omega\times\mathcal{T}, \quad \eta=\bar\eta\quad\text{on }\partial_\eta\Omega\times\mathcal{T}, }[/math]
- [math]\displaystyle{ \quad -(\varepsilon^2_\eta\nabla\,\eta)\cdot m = q\quad\text{on } \partial_q \Omega \times \mathcal{T}, \quad \eta=\eta_o \quad\text{on } \Omega\times\{0\}, }[/math]
where [math]\displaystyle{ M_{\eta} }[/math] is the mobility, [math]\displaystyle{ f }[/math] is a double-well potential, [math]\displaystyle{ \bar\eta }[/math] is the control on the state variable at the portion of the boundary [math]\displaystyle{ \partial_\eta\Omega }[/math], [math]\displaystyle{ q }[/math] is the source control at [math]\displaystyle{ \partial_q\Omega }[/math], [math]\displaystyle{ \eta_o }[/math] is the initial condition, and [math]\displaystyle{ m }[/math] is the outward normal to [math]\displaystyle{ \partial\Omega }[/math].
It is the L2 gradient flow of the Ginzburg–Landau free energy functional.[3] It is closely related to the Cahn–Hilliard equation.
Mathematical description
Let
- [math]\displaystyle{ \Omega\subset \R^n }[/math] be an open set,
- [math]\displaystyle{ v_0(x)\in L^2(\Omega) }[/math] an arbitrary initial function,
- [math]\displaystyle{ \varepsilon\gt 0 }[/math] and [math]\displaystyle{ T\gt 0 }[/math] two constants.
A function [math]\displaystyle{ v(x,t):\Omega\times [0,T]\to \R }[/math] is a solution to the Allen–Cahn equation if it solves[4]
- [math]\displaystyle{ \partial_t v-\Delta_x v = \frac{1}{\varepsilon^2}f(v),\quad \Omega \times[0,T] }[/math]
where
- [math]\displaystyle{ \Delta_x }[/math] is the Laplacian with respect to the space [math]\displaystyle{ x }[/math],
- [math]\displaystyle{ f(v)=F'(v) }[/math] is the derivative of a non-negative [math]\displaystyle{ F\in C^1(\R) }[/math] with two minima [math]\displaystyle{ F(\pm 1)=0 }[/math].
Usually, one has the following initial condition with the Neumann boundary condition
- [math]\displaystyle{ \begin{cases} v(x,0) = v_0(x), & \Omega \times \{0\}\\ \partial_n v = 0, & \partial \Omega \times [0,T]\\ \end{cases} }[/math]
where [math]\displaystyle{ \partial_n v }[/math] is the outer normal derivative.
For [math]\displaystyle{ F(v) }[/math] one popular candidate is
- [math]\displaystyle{ F(v)=\frac{(v^2-1)^2}{4},\qquad f(v)=v^3-v. }[/math]
References
- ↑ Allen, S. M.; Cahn, J. W. (1972). "Ground State Structures in Ordered Binary Alloys with Second Neighbor Interactions". Acta Metall. 20 (3): 423–433. doi:10.1016/0001-6160(72)90037-5.
- ↑ Allen, S. M.; Cahn, J. W. (1973). "A Correction to the Ground State of FCC Binary Ordered Alloys with First and Second Neighbor Pairwise Interactions". Scripta Metallurgica 7 (12): 1261–1264. doi:10.1016/0036-9748(73)90073-2.
- ↑ Veerman, Frits (March 8, 2016). "What is the L2 gradient flow?". MathOverflow. https://math.stackexchange.com/q/1688383.
- ↑ Bartels, Sören (2015). Numerical Methods for Nonlinear Partial Differential Equations. Deutschland: Springer International Publishing. p. 153.
Further reading
- http://www.ctcms.nist.gov/~wcraig/variational/node10.html
- Allen, S. M.; Cahn, J. W. (1975). "Coherent and Incoherent Equilibria in Iron-Rich Iron-Aluminum Alloys". Acta Metall. 23 (9): 1017. doi:10.1016/0001-6160(75)90106-6.
- Allen, S. M.; Cahn, J. W. (1976). "On Tricritical Points Resulting from the Intersection of Lines of Higher-Order Transitions with Spinodals". Scripta Metallurgica 10 (5): 451–454. doi:10.1016/0036-9748(76)90171-x.
- Allen, S. M.; Cahn, J. W. (1976). "Mechanisms of Phase Transformation Within the Miscibility Gap of Fe-Rich Fe-Al Alloys". Acta Metall. 24 (5): 425–437. doi:10.1016/0001-6160(76)90063-8.
- Cahn, J. W.; Allen, S. M. (1977). "A Microscopic Theory of Domain Wall Motion and Its Experimental Verification in Fe-Al Alloy Domain Growth Kinetics". Journal de Physique 38: C7–51.
- Allen, S. M.; Cahn, J. W. (1979). "A Microscopic Theory for Antiphase Boundary Motion and Its Application to Antiphase Domain Coarsening". Acta Metall. 27 (6): 1085–1095. doi:10.1016/0001-6160(79)90196-2.
- Bronsard, L.; Reitich, F. (1993). "On three-phase boundary motion and the singular limit of a vector valued Ginzburg–Landau equation". Arch. Rat. Mech. Anal. 124 (4): 355–379. doi:10.1007/bf00375607. Bibcode: 1993ArRMA.124..355B.
External links
- Simulation by Nils Berglund of a solution of the Allen–Cahn equation
 |