Brahmagupta's formula
In Euclidean geometry, Brahmagupta's formula, named after the 7th century Indian mathematician, is used to find the area of any cyclic quadrilateral (one that can be inscribed in a circle) given the lengths of the sides. Its generalized version, Bretschneider's formula, can be used with non-cyclic quadrilateral. Heron's formula can be thought as a special case of the Brahmagupta's formula for triangles.
Formulation
Brahmagupta's formula gives the area K of a cyclic quadrilateral whose sides have lengths a, b, c, d as
- [math]\displaystyle{ K=\sqrt{(s-a)(s-b)(s-c)(s-d)} }[/math]
where s, the semiperimeter, is defined to be
- [math]\displaystyle{ s=\frac{a+b+c+d}{2}. }[/math]
This formula generalizes Heron's formula for the area of a triangle. A triangle may be regarded as a quadrilateral with one side of length zero. From this perspective, as d approaches zero, a cyclic quadrilateral converges into a cyclic triangle (all triangles are cyclic), and Brahmagupta's formula simplifies to Heron's formula.
If the semiperimeter is not used, Brahmagupta's formula is
- [math]\displaystyle{ K=\frac{1}{4}\sqrt{(-a+b+c+d)(a-b+c+d)(a+b-c+d)(a+b+c-d)}. }[/math]
Another equivalent version is
- [math]\displaystyle{ K=\frac{\sqrt{(a^2+b^2+c^2+d^2)^2+8abcd-2(a^4+b^4+c^4+d^4)}}{4}\cdot }[/math]
Proof
Trigonometric proof
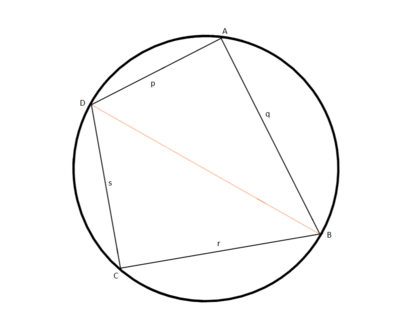
Here the notations in the figure to the right are used. The area K of the cyclic quadrilateral equals the sum of the areas of △ADB and △BDC:
- [math]\displaystyle{ K = \frac{1}{2}pq\sin A + \frac{1}{2}rs\sin C. }[/math]
But since □ABCD is a cyclic quadrilateral, ∠DAB = 180° − ∠DCB. Hence sin A = sin C. Therefore,
- [math]\displaystyle{ K = \frac{1}{2}pq\sin A + \frac{1}{2}rs\sin A }[/math]
- [math]\displaystyle{ K^2 = \frac{1}{4} (pq + rs)^2 \sin^2 A }[/math]
- [math]\displaystyle{ 4K^2 = (pq + rs)^2 (1 - \cos^2 A) = (pq + rs)^2 - ((pq + rs)\cos A)^2 }[/math]
(using the trigonometric identity).
Solving for common side DB, in △ADB and △BDC, the law of cosines gives
- [math]\displaystyle{ p^2 + q^2 - 2pq\cos A = r^2 + s^2 - 2rs\cos C. }[/math]
Substituting cos C = −cos A (since angles A and C are supplementary) and rearranging, we have
- [math]\displaystyle{ (pq + rs) \cos A = \frac{1}{2}(p^2 + q^2 - r^2 - s^2). }[/math]
Substituting this in the equation for the area,
- [math]\displaystyle{ 4K^2 = (pq + rs)^2 - \frac{1}{4}(p^2 + q^2 - r^2 - s^2)^2 }[/math]
- [math]\displaystyle{ 16K^2 = 4(pq + rs)^2 - (p^2 + q^2 - r^2 - s^2)^2. }[/math]
The right-hand side is of the form a2 − b2 = (a − b)(a + b) and hence can be written as
- [math]\displaystyle{ [2(pq + rs)) - p^2 - q^2 + r^2 +s^2][2(pq + rs) + p^2 + q^2 -r^2 - s^2] }[/math]
which, upon rearranging the terms in the square brackets, yields
- [math]\displaystyle{ 16K^2= [ (r+s)^2 - (p-q)^2 ][ (p+q)^2 - (r-s)^2 ] }[/math]
that can be factored again into
- [math]\displaystyle{ 16K^2=(q+r+s-p)(p+r+s-q)(p+q+s-r)(p+q+r-s). }[/math]
Introducing the semiperimeter S = p + q + r + s/2 yields
- [math]\displaystyle{ 16K^2 = 16(S-p)(S-q)(S-r)(S-s). }[/math]
Taking the square root, we get
- [math]\displaystyle{ K = \sqrt{(S-p)(S-q)(S-r)(S-s)}. }[/math]
Non-trigonometric proof
An alternative, non-trigonometric proof utilizes two applications of Heron's triangle area formula on similar triangles.[1]
Extension to non-cyclic quadrilaterals
In the case of non-cyclic quadrilaterals, Brahmagupta's formula can be extended by considering the measures of two opposite angles of the quadrilateral:
- [math]\displaystyle{ K=\sqrt{(s-a)(s-b)(s-c)(s-d)-abcd\cos^2\theta} }[/math]
where θ is half the sum of any two opposite angles. (The choice of which pair of opposite angles is irrelevant: if the other two angles are taken, half their sum is 180° − θ. Since cos(180° − θ) = −cos θ, we have cos2(180° − θ) = cos2 θ.) This more general formula is known as Bretschneider's formula.
It is a property of cyclic quadrilaterals (and ultimately of inscribed angles) that opposite angles of a quadrilateral sum to 180°. Consequently, in the case of an inscribed quadrilateral, θ is 90°, whence the term
- [math]\displaystyle{ abcd\cos^2\theta=abcd\cos^2 \left(90^\circ\right)=abcd\cdot0=0, }[/math]
giving the basic form of Brahmagupta's formula. It follows from the latter equation that the area of a cyclic quadrilateral is the maximum possible area for any quadrilateral with the given side lengths.
A related formula, which was proved by Coolidge, also gives the area of a general convex quadrilateral. It is[2]
- [math]\displaystyle{ K=\sqrt{(s-a)(s-b)(s-c)(s-d)-\textstyle{1\over4}(ac+bd+pq)(ac+bd-pq)} }[/math]
where p and q are the lengths of the diagonals of the quadrilateral. In a cyclic quadrilateral, pq = ac + bd according to Ptolemy's theorem, and the formula of Coolidge reduces to Brahmagupta's formula.
Related theorems
- Heron's formula for the area of a triangle is the special case obtained by taking d = 0.
- The relationship between the general and extended form of Brahmagupta's formula is similar to how the law of cosines extends the Pythagorean theorem.
- Increasingly complicated closed-form formulas exist for the area of general polygons on circles, as described by Maley et al.[3]
References
- ↑ Hess, Albrecht, "A highway from Heron to Brahmagupta", Forum Geometricorum 12 (2012), 191–192.
- ↑ J. L. Coolidge, "A Historically Interesting Formula for the Area of a Quadrilateral", American Mathematical Monthly, 46 (1939) pp. 345-347.
- ↑ Maley, F. Miller; Robbins, David P.; Roskies, Julie (2005). "On the areas of cyclic and semicyclic polygons". Advances in Applied Mathematics 34 (4): 669–689. doi:10.1016/j.aam.2004.09.008.
External links
- A geometric proof from Sam Vandervelde.
- Brahmagupta's formula at ProofWiki
- Weisstein, Eric W.. "Brahmagupta's Formula". http://mathworld.wolfram.com/BrahmaguptasFormula.html.
 |