Cramer–Castillon problem
In geometry, the Cramer–Castillon problem is a problem stated by the Swiss mathematician Gabriel Cramer solved by the Italian mathematician, resident in Berlin, Jean de Castillon in 1776.[1]
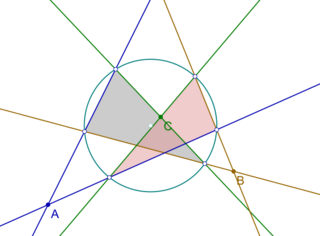
The problem consists of (see the image):
Given a circle [math]\displaystyle{ Z }[/math] and three points [math]\displaystyle{ A, B, C }[/math] in the same plane and not on [math]\displaystyle{ Z }[/math], to construct every possible triangle inscribed in [math]\displaystyle{ Z }[/math] whose sides (or their elongations) pass through [math]\displaystyle{ A, B, C }[/math] respectively.
Centuries before, Pappus of Alexandria had solved a special case: when the three points are collinear. But the general case had the reputation of being very difficult.[2]
After the geometrical construction of Castillon, Lagrange found an analytic solution, easier than Castillon's. In the beginning of the 19th century, Lazare Carnot generalized it to [math]\displaystyle{ n }[/math] points.[3]
References
Bibliography
- Dieudonné, Jean (1992). "Some problems in Classical Mathematics". Mathematics — The Music of Reason. Springer. pp. 77–101. doi:10.1007/978-3-662-35358-5_5. ISBN 978-3-642-08098-2. https://link.springer.com/book/10.1007/978-3-662-35358-5.
- Ostermann, Alexander; Wanner, Gerhard (2012). "6.9 The Cramer–Castillon problem". Geometry by Its History. Springer. pp. 175–178. ISBN 978-3-642-29162-3. https://books.google.com/books?id=eOSqPHwWJX8C.
- Wanner, Gerhard (2006). "The Cramer–Castillon problem and Urquhart's 'most elementary´ theorem". Elemente der Mathematik 61 (2): 58–64. doi:10.4171/EM/33. ISSN 0013-6018.
External links
- Stark, Maurice (2002). "Castillon's problem". http://wwwedu.ge.ch/cptic/clubs/cabri/download/lettre96/Preuve_Starck.pdf.
 |