Physics:Capstan equation
The capstan equation[1] or belt friction equation, also known as Euler-Eytelwein formula[2] (after Leonhard Euler and Johann Albert Eytelwein),[3] relates the hold-force to the load-force if a flexible line is wound around a cylinder (a bollard, a winch or a capstan).[4][1]
It also applies for fractions of one turn as occur with rope drives or band brakes.
Because of the interaction of frictional forces and tension, the tension on a line wrapped around a capstan may be different on either side of the capstan. A small holding force exerted on one side can carry a much larger loading force on the other side; this is the principle by which a capstan-type device operates.
A holding capstan is a ratchet device that can turn only in one direction; once a load is pulled into place in that direction, it can be held with a much smaller force. A powered capstan, also called a winch, rotates so that the applied tension is multiplied by the friction between rope and capstan. On a tall ship a holding capstan and a powered capstan are used in tandem so that a small force can be used to raise a heavy sail and then the rope can be easily removed from the powered capstan and tied off.
In rock climbing this effect allows a lighter person to hold (belay) a heavier person when top-roping, and also produces rope drag during lead climbing.
The formula is
- [math]\displaystyle{ T_\text{load} = T_\text{hold}\ e^{ \mu \phi} ~, }[/math]
where [math]\displaystyle{ T_\text{load} }[/math] is the applied tension on the line, [math]\displaystyle{ T_\text{hold} }[/math] is the resulting force exerted at the other side of the capstan, [math]\displaystyle{ \mu }[/math] is the coefficient of friction between the rope and capstan materials, and [math]\displaystyle{ \phi }[/math] is the total angle swept by all turns of the rope, measured in radians (i.e., with one full turn the angle [math]\displaystyle{ \phi =2\pi\, }[/math]).
For dynamic applications such as belt drives or brakes the quantity of interest is the force difference between [math]\displaystyle{ T_\text{load} }[/math] and [math]\displaystyle{ T_\text{hold} }[/math]. The formula for this is
- [math]\displaystyle{ F = T_\text{load} - T_\text{hold} = (e^{ \mu \phi} - 1) ~T_\text{hold} = (1 - e^{- \mu \phi}) ~T_\text{load} }[/math]
Several assumptions must be true for the equations to be valid:
- The rope is on the verge of full sliding, i.e. [math]\displaystyle{ T_\text{load} }[/math] is the maximum load that one can hold. Smaller loads can be held as well, resulting in a smaller effective contact angle [math]\displaystyle{ \phi }[/math].
- It is important that the line is not rigid, in which case significant force would be lost in the bending of the line tightly around the cylinder. (The equation must be modified for this case.) For instance a Bowden cable is to some extent rigid and doesn't obey the principles of the capstan equation.
- The line is non-elastic.
It can be observed that the force gain increases exponentially with the coefficient of friction, the number of turns around the cylinder, and the angle of contact. Note that the radius of the cylinder has no influence on the force gain.
The table below lists values of the factor [math]\displaystyle{ e^{ \mu \phi} \, }[/math] based on the number of turns and coefficient of friction μ.
| Number of turns |
Coefficient of friction μ | ||||||
|---|---|---|---|---|---|---|---|
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | |
| 0.5 | 1.4 | 1.9 | 2.6 | 3.5 | 4.8 | 6.6 | 9 |
| 1 | 1.9 | 3.5 | 6.6 | 12 | 23 | 43 | 81 |
| 2 | 3.5 | 12 | 43 | 152 | 535 | 1881 | 6661 |
| 3 | 6.6 | 43 | 286 | 1881 | 12392 | 81612 | 537503 |
| 4 | 12 | 152 | 1881 | 23228 | 286751 | 3540026 | 43702631 |
| 5 | 23 | 535 | 12392 | 286751 | 6635624 | 153552935 | 3553321281 |
From the table it is evident why one seldom sees a sheet (a rope to the loose side of a sail) wound more than three turns around a winch. The force gain would be extreme besides being counter-productive since there is risk of a riding turn, result being that the sheet will foul, form a knot and not run out when eased (by slacking grip on the tail (free end)).
It is both ancient and modern practice for anchor capstans and jib winches to be slightly flared out at the base, rather than cylindrical, to prevent the rope (anchor warp or sail sheet) from sliding down. The rope wound several times around the winch can slip upwards gradually, with little risk of a riding turn, provided it is tailed (loose end is pulled clear), by hand or a self-tailer.
For instance, the factor "153,552,935" (5 turns around a capstan with a coefficient of friction of 0.6) means, in theory, that a newborn baby would be capable of holding (not moving) the weight of two USS Nimitz supercarriers (97,000 tons each, but for the baby it would be only a little more than 1 kg). The large number of turns around the capstan combined with such a high friction coefficient mean that very little additional force is necessary to hold such heavy weight in place. The cables necessary to support this weight, as well as the capstan's ability to withstand the crushing force of those cables, are separate considerations.
Derivation
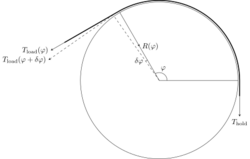
The applied tension [math]\displaystyle{ T_{\mathrm{load}}(\varphi) }[/math] is a function of the total angle subtended by the rope on the capstan. On the verge of slipping, this is also the frictional force, which is by definition [math]\displaystyle{ \mu }[/math] times the normal force [math]\displaystyle{ R(\varphi) }[/math]. By simple geometry, the additional normal force [math]\displaystyle{ \delta R(\varphi) = R(\varphi + \delta\varphi) - R(\varphi) }[/math] when increasing the angle by a small angle [math]\displaystyle{ \delta\varphi }[/math] is well approximated by [math]\displaystyle{ \delta R(\varphi)\approx T_\mathrm{load}(\varphi) \sin (\delta \varphi) \approx T_\mathrm{load}(\varphi)\delta\varphi }[/math]. Combining these and considering infinitesimally small [math]\displaystyle{ \delta \varphi }[/math] yields the differential equation
[math]\displaystyle{ \frac{d T_\mathrm{load}(\varphi)}{d \varphi} = \mu T_\mathrm{load}(\varphi),\qquad T_\mathrm{load}(0) = T_\mathrm{hold}, }[/math]
whose solution is
[math]\displaystyle{ T_\mathrm{load}(\varphi) = T_\mathrm{hold} e^{\mu\varphi} }[/math]
Generalizations
Generalization of the capstan equation for a V-belt
The belt friction equation for a v-belt is:
- [math]\displaystyle{ T_\text{load} = T_\text{hold}{e}^{\mu \phi / \sin( \alpha / 2 )} }[/math]
where [math]\displaystyle{ \alpha }[/math] is the angle (in radians) between the two flat sides of the pulley that the v-belt presses against.[5] A flat belt has an effective angle of [math]\displaystyle{ \alpha = \pi }[/math].
The material of a V-belt or multi-V serpentine belt tends to wedge into the mating groove in a pulley as the load increases, improving torque transmission.[6]
For the same power transmission, a V-belt requires less tension than a flat belt, increasing bearing life.[5]
Generalization of the capstan equation for a rope lying on an arbitrary orthotropic surface
If a rope is lying in equilibrium under tangential forces on a rough orthotropic surface then all three following conditions are satisfied:
- No separation – normal reaction [math]\displaystyle{ N }[/math] is positive for all points of the rope curve:
- [math]\displaystyle{ N=-k_nT\gt 0 }[/math], where [math]\displaystyle{ k_n }[/math] is a normal curvature of the rope curve.
- Dragging coefficient of friction [math]\displaystyle{ \mu_g }[/math] and angle [math]\displaystyle{ \alpha }[/math] are satisfying the following criteria for all points of the curve
- [math]\displaystyle{ -\mu_g\lt \tan \alpha \lt +\mu_g }[/math]
- Limit values of the tangential forces:
- The forces at both ends of the rope [math]\displaystyle{ T }[/math] and [math]\displaystyle{ T_0 }[/math] are satisfying the following inequality
- [math]\displaystyle{ T_0 e^{-\int_s \omega ds}\le T \le T_0 e^{\int_s \omega ds} }[/math]
- with [math]\displaystyle{ \omega = \mu_\tau \sqrt{ k_n^2 - \frac{k_g^2}{\mu_g^2}}=\mu_\tau k \sqrt{ \cos^2 \alpha - \frac{\sin^2 \alpha}{\mu_g^2}}, }[/math]
- where [math]\displaystyle{ k_g }[/math]is a geodesic curvature of the rope curve, [math]\displaystyle{ k }[/math] is a curvature of a rope curve, [math]\displaystyle{ \mu_\tau }[/math]is a coefficient of friction in the tangential direction.
- If [math]\displaystyle{ \omega = const }[/math] then [math]\displaystyle{ T_0 e^{-\mu_\tau k s \, \sqrt{ \cos^2 \alpha - \frac{\sin^2 \alpha}{\mu_g^2}}}\le T \le T_0 e^{\mu_\tau k s \, \sqrt{ \cos^2 \alpha - \frac{\sin^2 \alpha}{\mu_g^2}}}. }[/math]
This generalization has been obtained by Konyukhov.[7][8]
See also
- Belt friction
- Frictional contact mechanics
- Torque amplifier, a device that exploits the capstan effect
References
- ↑ 1.0 1.1 Attaway, Stephen W. (1999-11-01). "The Mechanics of Friction in Rope Rescue". International Tech Rescue Symposium. https://itrsonline.org/tproduct/1-969924084631-the-mechanics-of-friction-in-rope-rescue. Retrieved 23 Nov 2022.
- ↑ Metzger, Andreas; Konyukhov, Alexander; Schweizerhof, Karl (2011). "Finite Element implementation for the EULER-EYTELWEIN-problem and further use in FEM-simulation of common nautical knots". PAMM Proc. Appl. Math. Mech. 11: 249–250. doi:10.1002/pamm.201110116.
- ↑ Mann, Herman (5 May 2005). "Belt Friction". http://www.atp.ruhr-uni-bochum.de/rt1/currentcourse/node57.html.
- ↑ Johnson, K. L. (1985) (PDF). Contact Mechanics. http://www.knovel.com/web/portal/browse/display?_EXT_KNOVEL_DISPLAY_bookid=2685. Retrieved February 14, 2011.
- ↑ 5.0 5.1 Moradmand, Jamshid; Marcks, Russell; Looker, Tom. "Belt and Wrap Friction". http://statics.marcks.cc/friction/pdf/belt_friction.pdf.
- ↑ Slocum, Alexander (2008). "FUNdaMENTALS of Design". page 5-9. http://web.mit.edu/2.75/fundamentals/FUNdaMENTALs%20Book%20pdf/FUNdaMENTALs%20Topic%205.PDF.
- ↑ Konyukhov, Alexander (2015-04-01). "Contact of ropes and orthotropic rough surfaces" (in en). Journal of Applied Mathematics and Mechanics 95 (4): 406–423. doi:10.1002/zamm.201300129. ISSN 1521-4001. Bibcode: 2015ZaMM...95..406K.
- ↑ Konyukhov, A.; Izi, R.. "Introduction to Computational Contact Mechanics: A Geometrical Approach". Wiley. http://eu.wiley.com/WileyCDA/WileyTitle/productCd-111877065X,subjectCd-MA80.html.
Further reading
- Arne Kihlberg, Kompendium i Mekanik för E1, del II, Göteborg 1980, 60–62.
External links
 |