Physics:Hadronic shower
The hadronic showering process is dominated by a succession of inelastic hadronic interactions. At high energy, these are characterized by multiparticle production and particle emission originating from nuclear decay of excited nuclei. Due to the relatively frequent generation of ![]() 's, there is also an electromagnetic component present in hadronic showers.
's, there is also an electromagnetic component present in hadronic showers.
Secondaries are mostly pions and nucleons. The hadronic multiplication process is measured at the scale of nuclear interaction length ![]() , which is essentially energy-independent.
, which is essentially energy-independent.
Intrinsic limits on the energy resolution of hadronic calorimeters are:
- - A fluctuating
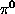 component among the secondaries which interacts electromagnetically without any further nuclear interaction (
component among the secondaries which interacts electromagnetically without any further nuclear interaction ( 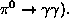 The average fraction of
The average fraction of 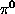 's is given by
's is given by 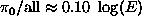 [E in GeV]. Showers may develop with a dominant electromagnetic component.
[E in GeV]. Showers may develop with a dominant electromagnetic component. - - A sizeable amount of the available energy is converted into excitation and breakup of nuclei. Only a small fraction of this energy will eventually appear as a detectable signal and with large event-to-event fluctuations.
- A considerable fraction of the energy of the incident particle is spent on reactions which do not result in an observable signal. Such processes may be energy leakage of various forms, like:
The average ratio between signals from electromagnetic and hadronic particles of the same incident energy is calorimeter- and energy-dependent; for a non-compensating calorimeter, one has typically
For possible improvements, ![]() Compensating Calorimeter.
Compensating Calorimeter.
At high energies some characteristic numbers of hadronic showers can be described by a simple parameterization in terms of ![]() (see Fabjan82:
(see Fabjan82:
shower maximum:
shower depth for 95% longitudinal containment:
shower radius for 95% radial containment:
Lengths are measured from the calorimeter face. For the average differential energy deposit over the volume of the cascade an acceptable longitudinal parametric approximation is given in Bock81:
with
A simple formula for the average lateral hadronic shower development is not in common use; double exponentials or combinations of exponentials with Gaussian curves have been applied with success (see Acosto92); superposition of two Breit-Wigner distributions has also been experimented with (Durston93). Average energy depositions allow one, in principle, to give an (average) energy density in three dimensions, which can be mapped onto any calorimeter cell structure; fluctuations can be added, but are a poor approximation to the reality of showers. A more realistic parameterization of shower fluctuations has been proposed by Iaselli92; in that model, the mean ![]() and standard deviation
and standard deviation ![]() , and their correlations, are parameterized for the energy in each layer of a sampling calorimeter. While this results in realistic showers, the method is applicable only for a specific calorimeter, and requires substantial preprocessing of fully simulated (or measured) showers.
, and their correlations, are parameterized for the energy in each layer of a sampling calorimeter. While this results in realistic showers, the method is applicable only for a specific calorimeter, and requires substantial preprocessing of fully simulated (or measured) showers.
Contrary to electromagnetic showers, which develop in subnanosecond time, the physics of hadronic showers is characterized by different time scales, the slowest of which (de-excitation of heavy nuclei) may reach a microsecond (see Caldwell93).


