Pregroup grammar
Pregroup grammar (PG) is a grammar formalism intimately related to categorial grammars. Much like categorial grammar (CG), PG is a kind of type logical grammar. Unlike CG, however, PG does not have a distinguished function type. Rather, PG uses inverse types combined with its monoidal operation.
Definition of a pregroup
A pregroup is a partially ordered algebra such that is a monoid, satisfying the following relations:
- (contraction)
- (expansion)
The contraction and expansion relations are sometimes called Ajdukiewicz laws.
From this, it can be proven that the following equations hold:
and are called the left and right adjoints of x, respectively.
The symbols and are also written and respectively. In category theory, pregroups are also known as autonomous categories[1] or (non-symmetric) compact closed categories.[2] More typically, will just be represented by adjacency, i.e. as .
Definition of a pregroup grammar
A pregroup grammar consists of a lexicon of words (and possibly morphemes) L, a set of atomic types T which freely generates a pregroup, and a relation that relates words to types. In simple pregroup grammars, typing is a function that maps words to only one type each.
Examples
Some simple, intuitive examples using English as the language to model demonstrate the core principles behind pregroups and their use in linguistic domains.
Let L = {John, Mary, the, dog, cat, met, barked, at}, let T = {N, S, N0}, and let the following typing relation hold:
A sentence S that has type T is said to be grammatical if . We can prove this by use of a chain of . For example, we can prove that is grammatical by proving that :
by first using contraction on and then again on . A more convenient notation exists, however, that indicates contractions by connecting them with a drawn link between the contracting types (provided that the links are nested, i.e. don't cross). Words are also typically placed above their types to make the proof more intuitive. The same proof in this notation is simply
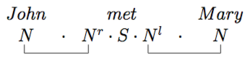
A more complex example proves that the dog barked at the cat is grammatical:
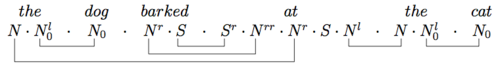
Historical notes
Pregroup grammars were introduced by Joachim Lambek in 1993 as a development of his syntactic calculus, replacing the quotients by adjoints.[3] Such adjoints had already been used earlier by Harris but without iterated adjoints and expansion rules. Adding such adjoints was interesting to handle more complex linguistic cases, where the fact that is needed. It was also motivated by a more algebraic viewpoint: the definition of a pregroup is a weakening of that of a group, introducing a distinction between the left and right inverses and replacing the equality by an order. This weakening was needed because using types from a free group would not work: an adjective would get the type , hence it could be inserted at any position in the sentence.[4]
Pregroup grammars have then been defined and studied for various languages (or fragments of them) including English,[5] Italian,[6] French,[7] Persian[8] and Sanskrit.[9] Languages with a relatively free word order such as Sanskrit required to introduce commutation relations to the pregroup, using precyclicity.
Semantics of pregroup grammars
Because of the lack of function types in PG, the usual method of giving a semantics via the λ-calculus or via function denotations is not available in any obvious way. Instead, two different methods exist, one purely formal method that corresponds to the λ-calculus, and one denotational method analogous to (a fragment of) the tensor mathematics of quantum mechanics.
Purely formal semantics
The purely formal semantics for PG consists of a logical language defined according to the following rules:
- Given a set of atomic terms T = {a, b, ...} and atomic function symbols F = {fm, gn, ...} (where subscripts are meta-notational indicating arity), and variables x, y, ..., all constants, variables, and well-formed function applications are basic terms (a function application is well-formed when the function symbol is applied to the appropriate number of arguments, which can be drawn from the atomic terms, variables, or can be other basic terms)
- Any basic term is a term
- Given any variable x, [x] is a term
- Given any terms m and n, is a term
Some examples of terms are f(x), g(a,h(x,y)), . A variable x is free in a term t if [x] does not appear in t, and a term with no free variables is a closed term. Terms can be typed with pregroup types in the obvious manner.
The usual conventions regarding α conversion apply.
For a given language, we give an assignment I that maps typed words to typed closed terms in a way that respects the pregroup structure of the types. For the English fragment given above we might therefore have the following assignment (with the obvious, implicit set of atomic terms and function symbols):
where E is the type of entities in the domain, and T is the type of truth values.
Together with this core definition of the semantics of PG, we also have a reduction rules that are employed in parallel with the type reductions. Placing the syntactic types at the top and semantics below, we have
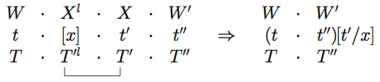
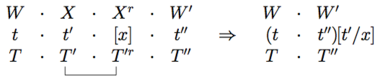
For example, applying this to the types and semantics for the sentence (emphasizing the link being reduced)
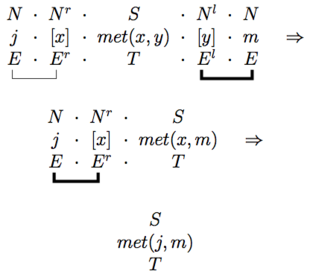
For the sentence :

See also
- Compact closed category
- Lambek calculus
References
- Lambek, Joachim (2008). "Pregroup grammars and Chomsky's earliest examples". Journal of Logic, Language and Information 17 (2): 141–160. doi:10.1007/s10849-007-9053-2. http://www.math.mcgill.ca/barr/lambek/pdffiles/Pregrammars.pdf.
- Preller, Anna (2007). "Semantic pregroup grammars handle long distance dependencies in French". Manuscript. http://hal-lirmm.ccsd.cnrs.fr/docs/00/15/43/98/PDF/SemanticPregroupGrammars.pdf.
- Claudia Casadio (2004), Pregroup Grammar. Theory and Applications
- ↑ Selinger, Peter (2011). "A survey of graphical languages for monoidal categories". 813. Springer. pp. 289–233. Bibcode: 2009arXiv0908.3347S.
- ↑ Preller, Anne; Mehrnoosh Sadrzadeh (2011). "Semantic Vector Models and Functional Models for Pregroup Grammars". Journal of Logic, Language and Information 20 (4): 419–443. doi:10.1007/s10849-011-9132-2. http://hal-lirmm.ccsd.cnrs.fr/docs/00/59/79/23/PDF/SemanticVectorModelsJLLI.pdf.
- ↑ Lambek, Joachim (1999). "Type Grammar revisited". 1582. Heidelberg: Springer. pp. 1–27.
- ↑ Lambek, Joachim (2008). "Pregroup Grammars and Chomsky's Earliest Examples". Journal of Logic, Language and Information 17 (2): 141–160. doi:10.1007/s10849-007-9053-2. http://www.math.mcgill.ca/barr/lambek/pdffiles/Pregrammars.pdf.
- ↑ Lambek 2008
- ↑ Casadio, Claudia; Joachim Lambek (2001). "An algebraic analysis of clitic pronouns in Italian". Logical Aspects of Computational Linguistics. Springer. pp. 110–124. ISBN 3540422730.
- ↑ Preller, Anne et al. (2008). "Pregroup grammars with linear parsing of the French verb phrase". CL2008: 53–84. http://hal-lirmm.ccsd.cnrs.fr/docs/00/30/65/04/PDF/PrellerPrince-LinearParsing.pdf.
- ↑ Sadrzadeh, Mehrnoosh (2008). "Pregroup analysis of Persian sentences". Computational Algebraic Approaches to Natural Language, Polimetrica, Milano, Italy: 121–144.
- ↑ Casadio, Claudia; Mehrnoosh Sadrzadeh (2014). "Word Order Alternation in Sanskrit via Precyclicity in Pregroup Grammars". Horizons of the Mind. A Tribute to Prakash Panangaden. Lecture Notes in Computer Science. 8464. Springer International Publishing. pp. 229–249. ISBN 978-3-319-06879-4.
 |
