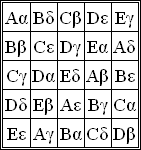| Display title | Graeco-Latin square |
| Default sort key | Graeco-Latin Square |
| Page length (in bytes) | 16,304 |
| Namespace ID | 0 |
| Page ID | 178352 |
| Page content language | en - English |
| Page content model | wikitext |
| Indexing by robots | Allowed |
| Number of redirects to this page | 0 |
| Counted as a content page | Yes |
| Page image |  |
| HandWiki item ID | None |
| Edit | Allow all users (infinite) |
| Move | Allow all users (infinite) |
| Page creator | imported>John Marlo |
| Date of page creation | 15:38, 19 November 2022 |
| Latest editor | imported>John Marlo |
| Date of latest edit | 15:38, 19 November 2022 |
| Total number of edits | 1 |
| Recent number of edits (within past 90 days) | 0 |
| Recent number of distinct authors | 0 |
Description | Content |
Article description: (description)
This attribute controls the content of the description and og:description elements. | In combinatorics, a Graeco-Latin square or Euler square or pair of orthogonal Latin squares of order n over two sets S and T, each consisting of n symbols, is an n×n arrangement of cells, each cell containing an ordered pair (s,t), where s is in S and t is in T, such that every row and every column contains... |