Lamination (topology): Difference between revisions
From HandWiki
imported>TextAI (add) |
(No difference)
|
Latest revision as of 05:36, 26 October 2021
Short description: Partitioned topological space
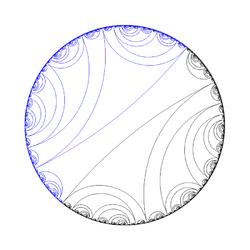
Lamination of rabbit Julia set
In topology, a branch of mathematics, a lamination is a :
- "topological space partitioned into subsets"[1]
- decoration (a structure or property at a point) of a manifold in which some subset of the manifold is partitioned into sheets of some lower dimension, and the sheets are locally parallel.
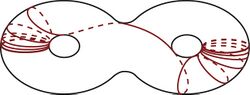
A lamination of a surface is a partition of a closed subset of the surface into smooth curves.
It may or may not be possible to fill the gaps in a lamination to make a foliation.[2]
Examples
- A geodesic lamination of a 2-dimensional hyperbolic manifold is a closed subset together with a foliation of this closed subset by geodesics.[3] These are used in Thurston's classification of elements of the mapping class group and in his theory of earthquake maps.
- Quadratic laminations, which remain invariant under the angle doubling map.[4] These laminations are associated with quadratic maps.[5][6] It is a closed collection of chords in the unit disc.[7] It is also topological model of Mandelbrot or Julia set.
See also
Notes
- ↑ Hazewinkel, Michiel, ed. (2001), "Lamination", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Main_Page
- ↑ "Defs.txt". Archived from the original on 2009-07-13. https://web.archive.org/web/20090713073050/http://www.ornl.gov/sci/ortep/topology/defs.txt. Retrieved 2009-07-13. Oak Ridge National Laboratory
- ↑ Laminations and foliations in dynamics, geometry and topology: proceedings of the conference on laminations and foliations in dynamics, geometry and topology, May 18-24, 1998, SUNY at Stony Brook
- ↑ Houghton, Jeffrey. "Useful Tools in the Study of Laminations" Paper presented at the annual meeting of the Mathematical Association of America MathFest, Omni William Penn, Pittsburgh, PA, Aug 05, 2010
- ↑ Tomoki KAWAHIRA: Topology of Lyubich-Minsky's laminations for quadratic maps: deformation and rigidity (3 heures)
- ↑ Topological models for some quadratic rational maps by Vladlen Timorin
- ↑ Modeling Julia Sets with Laminations: An Alternative Definition by Debra Mimbs
References
 |