Nesting algorithm: Difference between revisions
From HandWiki
imported>QCDvac link |
add |
||
| Line 1: | Line 1: | ||
{{Short description|Optimizing algorithm}} | |||
[[Image:NestingTypes01.jpg|thumb|right|Pictorial representations of three different types of nesting algorithms: Linear, Plate and Packing]] | [[Image:NestingTypes01.jpg|thumb|right|Pictorial representations of three different types of nesting algorithms: Linear, Plate and Packing]] | ||
'''Nesting algorithms''' are used to make the [[Engineering:Nesting (process)|most efficient use]] of material or space by evaluating many different possible combinations via [[Recursion (computer science)|recursion]]. | '''Nesting algorithms''' are used to make the [[Engineering:Nesting (process)|most efficient use]] of material or space. This could for instance be done by evaluating many different possible combinations via [[Recursion (computer science)|recursion]]. | ||
#Linear (1-dimensional): The simplest of the algorithms illustrated here. For an existing set there is only one position where a new cut can be placed – at the end of the last cut. Validation of a combination involves a simple Stock - Yield - Kerf = Scrap calculation. | #Linear (1-dimensional): The simplest of the algorithms illustrated here. For an existing set there is only one position where a new cut can be placed – at the end of the last cut. Validation of a combination involves a simple Stock - Yield - Kerf = Scrap calculation. | ||
Latest revision as of 19:24, 11 February 2026
Short description: Optimizing algorithm
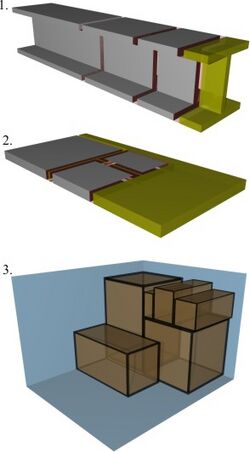
Nesting algorithms are used to make the most efficient use of material or space. This could for instance be done by evaluating many different possible combinations via recursion.
- Linear (1-dimensional): The simplest of the algorithms illustrated here. For an existing set there is only one position where a new cut can be placed – at the end of the last cut. Validation of a combination involves a simple Stock - Yield - Kerf = Scrap calculation.
- Plate (2-dimensional): These algorithms are significantly more complex. For an existing set, there may be as many as eight positions where a new cut may be introduced next to each existing cut, and if the new cut is not perfectly square then different rotations may need to be checked. Validation of a potential combination involves checking for intersections between two-dimensional objects.[1]
- Packing (3-dimensional): These algorithms are the most complex illustrated here due to the larger number of possible combinations. Validation of a potential combination involves checking for intersections between three-dimensional objects.
References
- ↑ 1.0 1.1 Herrmann, Jeffrey; Delalio, David. "Algorithms for Sheet Metal Nesting". IEEE TRANSACTIONS ON ROBOTICS AND AUTOMATION. http://www.isr.umd.edu/Labs/CIM/projects/nesting/sheetmetal.pdf. Retrieved 29 August 2015.
 |
