Carnot's theorem

[math]\displaystyle{ \begin{align} & {} \qquad DG + DH + DF \\ & {} = |DG| + |DH| - |DF| \\ & {} = R + r \end{align} }[/math]

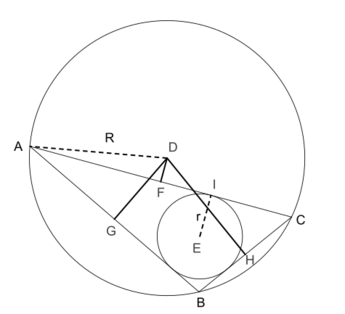
In Euclidean geometry, Carnot's theorem states that the sum of the signed distances from the circumcenter D to the sides of an arbitrary triangle ABC is

[math]\displaystyle{ DF + DG + DH = R + r,\ }[/math]

where r is the inradius and R is the circumradius of the triangle. Here the sign of the distances is taken to be negative if and only if the open line segment DX (X = F, G, H) lies completely outside the triangle. In the diagram, DF is negative and both DG and DH are positive.

The theorem is named after Lazare Carnot (1753–1823). It is used in a proof of the Japanese theorem for concyclic polygons.

External links

• Weisstein, Eric W.. "Carnot's theorem". http://mathworld.wolfram.com/CarnotsTheorem.html. 
• Carnot's Theorem at cut-the-knot
• Carnot's Theorem by Chris Boucher. The Wolfram Demonstrations Project.