Quasi-triangulation
From HandWiki
Revision as of 11:29, 8 March 2021 by imported>AstroAI (url)
A quasi-triangulation is a subdivision of a geometric object into simplices, where vertices are not points but arbitrary sloped line segments.[1] This division is not a triangulation in the geometric sense. It is a topological triangulation, however. A quasi-triangulation may have some of the characteristics of a Delaunay triangulation.
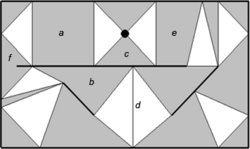
Quasi-triangulation. Line segments of the topology (quasi-vertices) are shown in black, gray — quasi-edges, white — faces. a — a convex quadrangular edge, b — a nonconvex quadrangular edge, c — a triangular edge, d — a degenerate edge, a and e — parallel edges, f — a quasi-edge contains a part of the line segment.
References
- ↑ Luzin S.Y.; Lyachek Y.T.; Petrosyan G.S.; Polubasov O.B. (2010). Models and algorithms for automated design of electronic and computer equipment (in Russian). BHV-Petersburg. pp. 224. ISBN 978-5-9775-0576-5.
 |

