Addition in quadrature
Addition in quadrature is a mathematical operation to combine the magnitude of two or more uncorrelated signals, such as independent uncertainties in propagation of uncertainty.
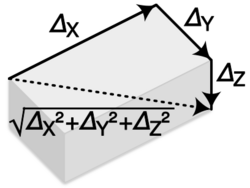
If measurements X, Y, Z, ... have independent errors ΔX, ΔY, ΔZ, ..., respectively, the quadrature method gives the overall error,
- [math]\displaystyle{ \varDelta_o = \sqrt{{\varDelta_X}^2 + {\varDelta_Y}^2 + {\varDelta_Z}^2 + ...} }[/math]
whereas the upper limit of the overall error is
- [math]\displaystyle{ \varDelta_u = {\varDelta_X} + {\varDelta_Y} + {\varDelta_Z} + ... }[/math]
if the errors were not independent.[1]
This is equivalent of finding the magnitude of the resultant of adding orthogonal vectors, each with magnitude equal to the uncertainty, using the Pythagorean theorem.
Some authors use the symbol ⊕ for addition in quadrature.[2][3]
Noise
In signal processing, addition in quadrature is used to find the overall noise from independent sources of noise. For example, if an image sensor gives 6 digital numbers of shot noise, 3 of dark current noise and 2 of Johnson–Nyquist noise under a specific condition, the overall noise,
- [math]\displaystyle{ \sigma = 6 \oplus 3 \oplus 2 = \sqrt{6^2 + 3^2 + 2^2} = 7 }[/math]
digital numbers,[4] showing the dominance of larger sources of noise.
References
- ↑ D.B. Schneider, Error Analysis in Measuring Systems, Proceedings of the 1962 Standards Laboratory Conference, page 94
- ↑ C. White et al, Diamond detectors for high energy physics, Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment Volume 351, Issue 1, 15 November 1994, Pages 217-221
- ↑ Qamar Ulhassan, Measurement of the ratio of top pair production cross section σ(13 TeV)/σ(8 TeV), CERN CMSPublic Web, 2017-04-27
- ↑ J.T. Bushberg et al, The Essential Physics of Medical Imaging, section 10.2.7, Wolters Kluwer Health