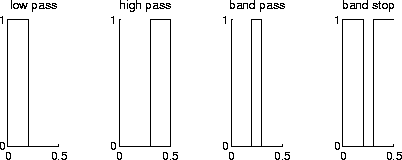Filtering
Filtering is a basic technique in signal processing, and usually consists of the modifications of the frequency components of a signal; for instance, the shape of the frequency spectrum is modified by suppressing or enhancing certain frequencies. In general, these filters are defined as step functions in the frequency domain (pass- and stop-bands).
Many linear shift-invariant systems can be described by a difference equation with constant coefficients of the form:
If we assume ![]() , we can compute the current output yn from the input values and output values that have been previously computed:
, we can compute the current output yn from the input values and output values that have been previously computed:
If N = 0, the filter is called a finite impulse response filter (FIR); the output depends only on the sum of products of weights bm with the present and past M input samples; this is a non-recursive filter. If M = 0 the filter is called an infinite impulse response filter (IIR); the output depends on the present input sample and the sum of products of weights bm with the present and past M input samples; this is a recursive filter.
Some idealized filters are shown in the following graph:
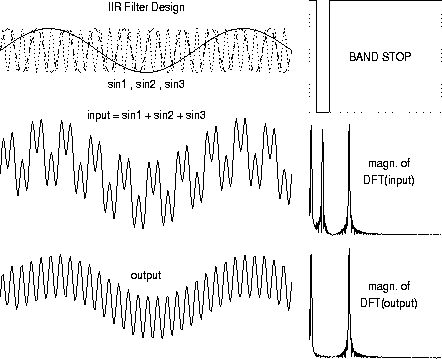
For the ![]() e.g. Kunt84, PROG79design of digital filters , or the signal processing tools of commercial mathematical packages. The following example of a band stop filter was constructed using Matlab MATLAB97:
e.g. Kunt84, PROG79design of digital filters , or the signal processing tools of commercial mathematical packages. The following example of a band stop filter was constructed using Matlab MATLAB97:
The graph shows an input signal consisting of the sum of three sine functions with different frequencies (sin1, sin2, sin3), the ideal band stop filter, and the resulting output signal with sin2 suppressed. The two plots of the magnitude of the digital Fourier transforms (DFT) of the input and output signals also show the suppression of the middle frequency.