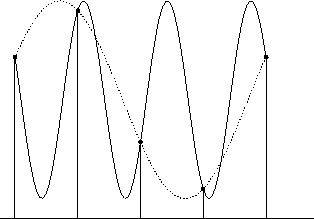
Sampling theorem

The greyvalues of digitized one- or two-dimensional signals are typically generated by an analogue-to-digital converter (ADC), by sampling a continuous signal at fixed intervals (e.g. in time), and quantizing (digitizing) the samples. The sampling (or point sampling) theorem states that a band-limited analogue signal x_a(t), i.e. a signal in a finite frequency band (e.g. between 0 and BHz), can be completely reconstructed from its samples x(n) = x(nT), if the sampling frequency is greater than 2B (the Nyquist rate); expressed in the time domain, this means that the sampling interval T is at most 1/2B seconds. Undersampling can produce serious errors (aliasing ) by introducing artefacts of low frequencies, both in one-dimensional signals and in digital images:

For more details and further reading , e.g. Kunt80 or Rabiner75.