Biography:Raoul Bricard
Raoul Bricard | |
|---|---|
 | |
| Born | 23 March 1870 |
| Died | 26 November 1943 (aged 73) |
| Scientific career | |
| Fields | Mathematics |
Raoul Bricard (23 March 1870 – 26 November 1943) was a French engineer and a mathematician. He is best known for his work in geometry, especially descriptive geometry and scissors congruence, and kinematics, especially mechanical linkages.
Biography
Bricard taught geometry at Ecole Centrale des Arts et Manufactures. In 1908 he became a professor of applied geometry at the National Conservatory of Arts and Crafts in Paris.[1] In 1932 he received the Poncelet Prize in mathematics from the Paris Academy of Sciences for his work in geometry.[2]
Work
In 1896 Bricard published a paper on Hilbert's third problem, even before the problem was stated by Hilbert.[3] In it he proved that mirror symmetric polytopes are scissors congruent, and proved a weak version of Dehn's criterion.
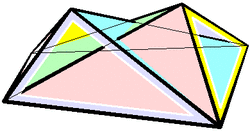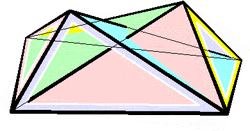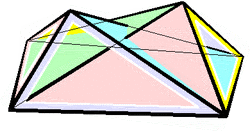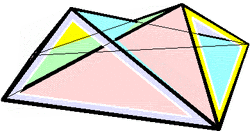
In 1897 Bricard published an important investigation on flexible polyhedra.[4] In it he classified all flexible octahedra, now known as Bricard octahedra.[5] This work was the subject of Henri Lebesgue's lectures in 1938.[6] Later Bricard discovered notable 6-bar linkages.[7][8]
Bricard also gave one of the first geometric proofs of Morley's trisector theorem in 1922.[9][10]
Books
Bricard authored six books, including a mathematics survey in Esperanto.[11] He is listed in Encyclopedia of Esperanto.[12]
- Matematika terminaro kaj krestomatio (in Esperanto), Hachette, Paris, 1905
- Géométrie descriptive, O. Doin et fils, 1911
- Cinématique et mécanismes, A. Colin, 1921
- Petit traité de perspective, Vuibert, 1924[13]
- Leçons de cinématique, Gauthier-Villars et cie., 1926
- Le calcul vectoriel, A. Colin, 1929
Notes
- ↑ Science, vol. 28 (1908), p. 707.
- ↑ "Prize Awards of the Paris Academy of Sciences", Nature vol. 131 (1933) 174-175.
- ↑ R. Bricard, "Sur une question de géométrie relative aux polyèdres", Nouvelles annales de mathématiques, Ser. 3, Vol. 15 (1896), 331-334.
- ↑ R. Bricard, Mémoire sur la théorie de l’octaèdre articulé , J. Math. Pures Appl., Vol. 3 (1897), 113–150 (see also the English translation and an alternative scan).
- ↑ P. Cromwell, Polyhedra, Cambridge University Press , 1997.
- ↑ Lebesgue H. (1967). "Octaedres articules de Bricard". Enseign. Math.. Series 2 13 (3): 175–185. doi:10.5169/seals-41541.
- ↑ K. Wohlhart, The two types of the orthogonal Bricard linkage, Mechanism and machine theory, vol. 28 (1993), 809-817.
- ↑ Bricard 6 Bar Linkage Origami on YouTube.
- ↑ Guy Richard K. (2007). "The Lighthouse Theorem, Morley & Malfatti - A Budget of Paradoxes". American Mathematical Monthly 114 (2): 97–141. doi:10.1080/00029890.2007.11920398. Archived from the original on April 19, 2012. https://web.archive.org/web/20120419064244/http://math.ucalgary.ca/files/publications/3414848.pdf.
- ↑ Alain Connes, "Symmetries", European Mathematical Society Newsletter No. 54 (December 2004).
- ↑ Raoul Bricard, from Open Library.
- ↑ Encyclopedia of Esperanto
- ↑ Emch, Arnold (1925). "Review: Petit Traité de Perspective by Raoul Bricard". Bull. Amer. Math. Soc. 31 (9): 564–565. doi:10.1090/s0002-9904-1925-04125-7. https://www.ams.org/journals/bull/1925-31-09/S0002-9904-1925-04125-7/S0002-9904-1925-04125-7.pdf.
References
- Laurent R., Raoul Bricard, Professeur de Géométrie appliquée aux arts, in Fontanon C., Grelon A. (éds.), Les professeurs du Conservatoire national des arts et métiers, dictionnaire biographique, 1794-1955, INRP-CNAM, Paris 1994, vol. 1, pp. 286–291.
External links
- Error in Template:Internet Archive author: Raoul Bricard doesn't exist.
 |

