Chemistry:Derjaguin approximation

Derjaguin approximation related the force between two spheres (top) and the interaction energy between two plates (bottom).

The Derjaguin approximation (or sometimes also referred to as the proximity approximation), named after the Russian scientist Boris Derjaguin, expresses the force profile acting between finite size bodies in terms of the force profile between two planar semi-infinite walls. This approximation is widely used to estimate forces between colloidal particles, as forces between two planar bodies are often much easier to calculate. The Derjaguin approximation expresses the force F(h) between two bodies as a function of the surface separation as

[math]\displaystyle{ F(h) = 2 \pi R_{\rm eff} W(h), }[/math]

where W(h) is the interaction energy per unit area between the two planar walls and R_eff the effective radius. When the two bodies are two spheres of radii R₁ and R₂, respectively, the effective radius is given by

[math]\displaystyle{ R_{\rm eff}^{-1} = R_1^{-1}+R_2^{-1}. }[/math]

Experimental force profiles between macroscopic bodies as measured with the surface forces apparatus (SFA) or colloidal probe technique are often reported as the ratio F(h)/R_eff.

Quantities involved and validity

The force F(h) between two bodies is related to the interaction free energy U(h) as

[math]\displaystyle{ F(h) = - {dU \over dh}, }[/math]

where h is the surface-to-surface separation. Conversely, when the force profile is known, one can evaluate the interaction energy as

[math]\displaystyle{ U(h) = \int_h^{\infty} F(h') \, dh'. }[/math]

When one considers two planar walls, the corresponding quantities are expressed per unit area. The disjoining pressure is the force per unit area and can be expressed by the derivative

[math]\displaystyle{ \Pi(h) = - {dW \over dh}, }[/math]

where W(h) is the surface free energy per unit area. Conversely, one has

[math]\displaystyle{ W(h) = \int_h^{\infty} \Pi(h') \, dh'. }[/math]

The main restriction of the Derjaguin approximation is that it is only valid at distances much smaller than the size of the objects involved, namely h ≪ R₁ and h ≪ R₂. Furthermore, it is a continuum approximation and thus valid at distances larger than the molecular length scale. Even when rough surfaces are involved, this approximation has been shown to be valid in many situations. Its range of validity is restricted to distances larger than the characteristic size of the surface roughness features (e.g., root mean square roughness).

Special cases

Frequently used geometries for the Derjaguin approximation. Two identical spheres, a planar wall and a sphere, and two perpendicularly crossing cylinders (left to right).

Frequent geometries considered involve the interaction between two identical spheres of radius R where the effective radius becomes

[math]\displaystyle{ R_{\rm eff} = R/2. }[/math]

In the case of interaction between a sphere of radius R and a planar surface, one has

[math]\displaystyle{ R_{\rm eff} = R. }[/math]

The above two relations can be obtained as special cases of the expression for R_eff given further above. For the situation of perpendicularly crossing cylinders as used in the surface forces apparatus, one has

[math]\displaystyle{ R_{\rm eff} = \sqrt{R_1R_2}, }[/math]

where R₁ and R₂ are the curvature radii of the two cylinders involved.

Simplified derivation

Explanations concerning the derivation of the Derjaguin approximation for two identical spheres.

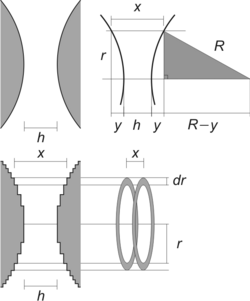
Consider the force F(h) between two identical spheres of radius R as an illustration. The surfaces of the two respective spheres are thought to be sliced into infinitesimal disks of width dr and radius r as shown in the figure. The force is given by the sum of the corresponding swelling pressures between the two disks

[math]\displaystyle{ F = \int \Pi(x) \, dA, }[/math]

where x is the distance between the disks and dA the area of one of these disks. This distance can be expressed as x=h+2y. By considering the Pythagorean theorem on the grey triangle shown in the figure one has

[math]\displaystyle{ R^2 = (R-y)^2+r^2. }[/math]

Expanding this expression and realizing that y ≪ R one finds that the area of the disk can be expressed as

[math]\displaystyle{ dA = 2 \pi r \, dr = 2 \pi R \, dy = \pi R \, dx . }[/math]

The force can now be written as

[math]\displaystyle{ F(h) = \pi R \int_h^{\infty} \Pi(x) \, dx = \pi R W(h), }[/math]

where W(h) is the surface free energy per unit area introduced above. When introducing the equation above, the upper integration limit was replaced by infinity, which is approximately correct as long as h ≪ R.

General case

In the general case of two convex bodies, the effective radius can be expressed as follows

[math]\displaystyle{ \frac{1}{R_{\rm eff}^2} = \left( \frac{1}{R'_{1}}+\frac{1}{R'_{2}} \right) \left( \frac{1}{R''_{1}}+\frac{1}{R''_{2}} \right) + \left( \frac{1}{R'_{1}}-\frac{1}{R''_{1}} \right) \left( \frac{1}{R'_{2}}-\frac{1}{R''_{2}} \right) \sin^2 \varphi, }[/math]

where R'_i and R"_i are the principal radii of curvature for the surfaces i = 1 and 2, evaluated at points of closest approach distance, and φ is the angle between the planes spanned by the circles with smaller curvature radii. When the bodies are non-spherical around the position of closest approach, a torque between the two bodies develops and is given by

[math]\displaystyle{ T = \pi R_{\rm eff}^{3} V(h) \left( \frac{1}{R'_{1}}-\frac{1}{R''_{1}} \right) \left( \frac{1}{R'_{2}}-\frac{1}{R''_{2}} \right) \sin 2 \varphi, }[/math]

where

[math]\displaystyle{ V(h) = \int_h^{\infty} W(h') \, dh'. }[/math]

The above expressions for two spheres are recovered by setting R'_i = R"_i = R_i. The torque vanishes in this case.

The expression for two perpendicularly crossing cylinders is obtained from R'_i = R_i and R"_i → ∞. In this case, torque will tend to orient the cylinders perpendicularly for repulsive forces. For attractive forces, the torque will tend to align them.

These general formulas have been used to evaluate approximate interaction forces between ellipsoids.

Beyond the Derjaguin approximation

The Derjaguin approximation is unique given its simplicity and generality. To improve this approximation, the surface element integration method as well as the surface integration approach were proposed to obtain more accurate expressions of the forces between two bodies. These procedures also considers the relative orientation of the approaching surfaces.

See also

• Atomic force microscopy
• Electrical double layer forces
• DLVO theory
• Van der Waals force

Further reading

• Zypman, F.R. (2006). "Exact expressions for colloidal plane–particle interaction forces and energies with applications to atomic force microscopy". J. Phys.: Condens. Matter 8 (10): 2795–2803. doi:10.1088/0953-8984/18/10/005. Bibcode: 2006JPCM...18.2795Z.