Dendrite (mathematics)
From HandWiki
Short description: Locally connected dendroid
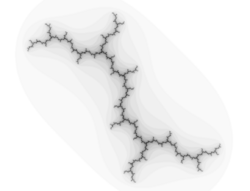
In mathematics, a dendrite is a certain type of topological space that may be characterized either as a locally connected dendroid or equivalently as a locally connected continuum that contains no simple closed curves.[1]
Importance
Dendrites may be used to model certain types of Julia set.[2] For example, if 0 is pre-periodic, but not periodic, under the function [math]\displaystyle{ f(z) = z^2 + c }[/math], then the Julia set of [math]\displaystyle{ f }[/math] is a dendrite: connected, without interior.[3]
References
- ↑ Analytic Topology, American Mathematical Society Colloquium Publications, 28, New York: American Mathematical Society, 1942, p. 88, https://books.google.com/books?id=niByQPkPObwC&pg=PA88.
- ↑ Carleson, Lennart; Gamelin, Theodore W. (1993), Complex Dynamics, Universitext, 69, Springer, p. 94, ISBN 9780387979427, https://books.google.com/books?id=M-I8qRE8HGUC&pg=PA94.
- ↑ An Introduction to Chaotic Dynamical Systems, Studies in Nonlinearity, Addison-Wesley Publishing Company, 1989, p. 294.
See also
- Misiurewicz point
- Real tree, a related concept defined using metric spaces instead of topological spaces
- Dendroid (topology) and unicoherent space, two more general types of tree-like topological space
 |