Star product

In mathematics, the star product is a method of combining graded posets with unique minimal and maximal elements, preserving the property that the posets are Eulerian.

Definition

The star product of two graded posets [math]\displaystyle{ (P,\le_P) }[/math] and [math]\displaystyle{ (Q,\le_Q) }[/math], where [math]\displaystyle{ P }[/math] has a unique maximal element [math]\displaystyle{ \widehat{1} }[/math] and [math]\displaystyle{ Q }[/math] has a unique minimal element [math]\displaystyle{ \widehat{0} }[/math], is a poset [math]\displaystyle{ P*Q }[/math] on the set [math]\displaystyle{ (P\setminus\{\widehat{1}\})\cup(Q\setminus\{\widehat{0}\}) }[/math]. We define the partial order [math]\displaystyle{ \le_{P*Q} }[/math] by [math]\displaystyle{ x\le y }[/math] if and only if:

1. [math]\displaystyle{ \{x,y\}\subset P }[/math], and [math]\displaystyle{ x\le_P y }[/math];

2. [math]\displaystyle{ \{x,y\}\subset Q }[/math], and [math]\displaystyle{ x\le_Q y }[/math]; or

3. [math]\displaystyle{ x\in P }[/math] and [math]\displaystyle{ y\in Q }[/math].

In other words, we pluck out the top of [math]\displaystyle{ P }[/math] and the bottom of [math]\displaystyle{ Q }[/math], and require that everything in [math]\displaystyle{ P }[/math] be smaller than everything in [math]\displaystyle{ Q }[/math].

Example

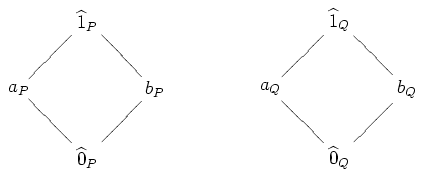
For example, suppose [math]\displaystyle{ P }[/math] and [math]\displaystyle{ Q }[/math] are the Boolean algebra on two elements.

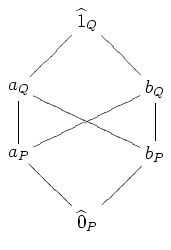
Then [math]\displaystyle{ P*Q }[/math] is the poset with the Hasse diagram below.

Properties

The star product of Eulerian posets is Eulerian.

See also

• Product order, a different way of combining posets

References

• Stanley, R., Flag [math]\displaystyle{ f }[/math]-vectors and the [math]\displaystyle{ \mathbf{cd} }[/math]-index, Math. Z. 216 (1994), 483-499.