Elementary comparison testing

Elementary comparison testing (ECT) is a white-box, control-flow, test-design methodology used in software development. The purpose of ECT is to enable detailed testing of complex software. Software code or pseudocode is tested to assess the proper handling of all decision outcomes. As with multiple-condition coverage and basis path testing, coverage of all independent and isolated conditions is accomplished through modified condition/decision coverage (MC/DC). Isolated conditions are aggregated into connected situations creating formal test cases. The independence of a condition is shown by changing the condition value in isolation. Each relevant condition value is covered by test cases.

Test case

A test case consists of a logical path through one or many decisions from start to end of a process. Contradictory situations are deduced from the test case matrix and excluded. The MC/DC approach isolates every condition, neglecting all possible subpath combinations and path coverage. [math]\displaystyle{ T=n+1 }[/math] where

• T is the number of test cases per decision and
• n the number of conditions.

The decision [math]\displaystyle{ d_i }[/math] consists of a combination of elementary conditions

[math]\displaystyle{ \begin{align} \Sigma &= \{0, 1\}\\ C&=\{c_0, c_1, c_2, c_3,..., c_n\} \end{align} }[/math] [math]\displaystyle{ \epsilon : C \to \Sigma \times C }[/math] [math]\displaystyle{ D \subseteq C^* \,;\; d_i \in D }[/math]

The transition function [math]\displaystyle{ \alpha }[/math] is defined as [math]\displaystyle{ \alpha : D \times \Sigma^* \to \Sigma \times D }[/math]

Given the transition [math]\displaystyle{ \vdash }[/math] [math]\displaystyle{ \vdash \subseteq (\Sigma \times D \times \Sigma^*) \times (\Sigma \times D \times \Sigma^*) }[/math]

[math]\displaystyle{ S_j=(b_j, d_m, v_j) \vdash (b_{j+1}, d_n, v_{j+1}) }[/math] [math]\displaystyle{ E_j=(a_j, c_j) \vdash (a_{j+1}, c_k) }[/math] [math]\displaystyle{ (b_{j+1}, d_n) = \alpha(d_m, v_j); (b_{j+1}, c_k) = \epsilon(c_j); a_j \in \Sigma, }[/math] the isolated test path [math]\displaystyle{ P_m }[/math] consists of [math]\displaystyle{ \begin{align} P_m &= (b_0, d_0, v_0) \vdash ... \vdash (b_i, d_i, v_i) \vdash^*(b_n, d_n, v_n) \\ &= (b_0, c_0) \vdash ... \vdash (b_m, c_m) \vdash^* (b_n, c_n) \end{align} }[/math] [math]\displaystyle{ b_i \in \Sigma; c_m \in d_i; v \in C^*; d_0=S; d_n=E. }[/math]

Test case graph

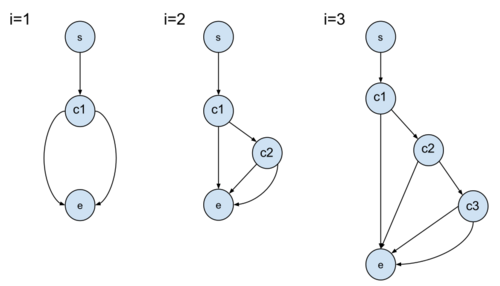
A test case graph illustrates all the necessary independent paths (test cases) to cover all isolated conditions. Conditions are represented by nodes, and condition values (situations) by edges. An edge addresses all program situations. Each situation is connected to one preceding and successive condition. Test cases might overlap due to isolated conditions.

Inductive proof of a number of condition paths

The elementary comparison testing method can be used to determine the number of condition paths by inductive proof.

Figure 2: ECT Inductive Proof Anchor

There are [math]\displaystyle{ r = 2^n }[/math] possible condition value combinations [math]\displaystyle{ \forall{i} \in \{1,...,n\},\ c_i\mapsto\{0,\ 1\}. }[/math]

When each condition [math]\displaystyle{ c_i }[/math] is isolated, the number of required test cases [math]\displaystyle{ T }[/math] per decision is: [math]\displaystyle{ T = \log_2(r)+1 = n + 1. }[/math]

Figure 3: ECT Inductive Proof End

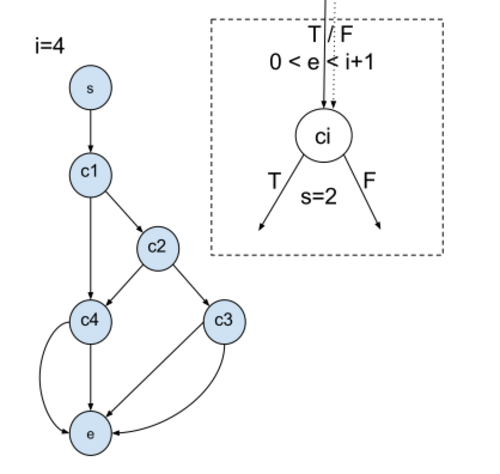
[math]\displaystyle{ \forall{i}\in\{1,...,n\} }[/math] there are [math]\displaystyle{ 0\lt e\lt i+1 }[/math] edges from parent nodes [math]\displaystyle{ c_i }[/math] and [math]\displaystyle{ s = 2 }[/math] edges to child nodes from [math]\displaystyle{ c_i }[/math].

Each individual condition [math]\displaystyle{ c_i }[/math] connects to at least one path [math]\displaystyle{ \forall{i}\in\{1,...,n-1\} , \ c_i\mapsto\{0,\ 1\} }[/math] from the maximal possible [math]\displaystyle{ n }[/math] connecting to [math]\displaystyle{ c_n }[/math] isolating [math]\displaystyle{ c_n }[/math].

All predecessor conditions [math]\displaystyle{ c_i;\ i\lt n }[/math] and respective paths are isolated. Therefore, when one node (condition) is added, the total number of paths, and required test cases, from start to finish increases by: [math]\displaystyle{ T = n-1+2 = n+1. }[/math] Q.E.D.

Test-case design steps

1. Identify decisions
2. Determine test situations per decision point (Modified Condition / Decision Coverage)
3. Create logical test-case matrix
4. Create physical test-case matrix

Example

Figure 4: ECT Example Control-Flow Graph

Figure 5: ECT Example D2 Conditions

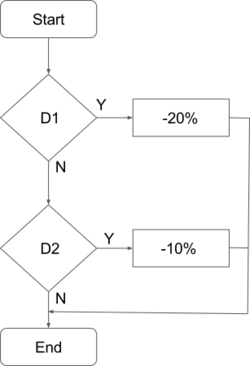
This example shows ETC applied to a holiday booking system. The discount system offers reduced-price vacations. The offered discounts are [math]\displaystyle{ -20\% }[/math] for members or for expensive vacations, [math]\displaystyle{ -10\% }[/math] for moderate vacations with workday departures, and [math]\displaystyle{ 0\% }[/math] otherwise. The example shows the creation of logical and physical test cases for all isolated conditions.

Pseudocode

if days > 15 or price > 1000 or member then
    return −0.2
else if (days > 8 and days ≤ 15 or price ≥ 500 and price ≤ 1000) and workday then
    return −0.1
else
    return 0.0

Factors

• Number of days: [math]\displaystyle{ \lt 8;\ 8-15;\ \gt 15 }[/math]
• Price (euros): [math]\displaystyle{ \lt 500;\ 500-1000;\ \gt 1000 }[/math]
• Membership card: none; silver; gold; platinum
• Departure date: workday; weekend; holiday

[math]\displaystyle{ T = 3 \times 3 \times 4 \times 3 = 108 }[/math] possible combinations (test cases).

Example in Python:

if days > 15 or price > 1000 or member:
    return -0.2
elif (days > 8 and days <= 15 or price >= 500 and price <= 1000) and workday:
    return -0.1
else:
    return 0.0

Step 1: Decisions

Table 1: Example D1 MC/DC

		Outcome
Decision D1		1			0
Conditions		c1	c2	c3	c1	c2	c3
c1	[math]\displaystyle{ \text{days}\gt 15 }[/math]	1	0	0	0	0	0
c2	[math]\displaystyle{ \text{price}\gt 1000 }[/math]	0	1	0	0	0	0
c3	[math]\displaystyle{ \text{member} }[/math]	0	0	1	0	0	0

[math]\displaystyle{ \begin{align} d_1 &= \text{days} \gt 15\ \text{or}\ \text{price} \gt 1000\ \text{Eur}\ \text{or}\ \text{member} \\ c_1 &= \text{days} \gt 15 \\ c_2 &= \text{price} \gt 1000 \\ c_3 &= \text{member} \\ \end{align} }[/math] [math]\displaystyle{ \begin{align} d_2 &= (8 \lt \text{days} \lt 15\ \text{or}\ 500 \lt \text{price} \lt 1000\ \text{Eur})\ \text{and}\ \text{workday} \\ c_4 &= 8 \lt \text{days} \lt 15 \\ c_5 &= 500 \lt \text{price} \lt 1000\ \text{Eur}\\ c_6 &= \text{workday} \\ \end{align} }[/math]

Step 2: MC/DC Matrix

Table 2: Example D2 MC/DC

		Outcome
Decision D2		1			0
Conditions		c4	c5	c6	c4	c5	c6
c4	[math]\displaystyle{ 8\lt \text{days}\lt 15 }[/math]	1	0	1	0	0	1
c5	[math]\displaystyle{ 500 \lt \text{price} \lt 1000 }[/math]	0	1	1	0	0	1
c6	[math]\displaystyle{ \text{workday} }[/math]	1	0	1	1	0	0

The highlighted diagonals in the MC/DC Matrix are describing the isolated conditions: [math]\displaystyle{ (c_i,c_i) \mapsto \{1,0\} }[/math] all duplicate situations are regarded as proven and removed.

Step 3: Logical test-Case matrix

Table 3: Example Logical Test Case Matrix

Situation [math]\displaystyle{ S_{j} }[/math]	[math]\displaystyle{ T_1 }[/math]	[math]\displaystyle{ T_2 }[/math]	[math]\displaystyle{ T_3 }[/math]	[math]\displaystyle{ T_4 }[/math]	[math]\displaystyle{ T_5 }[/math]	[math]\displaystyle{ T_6 }[/math]	[math]\displaystyle{ T_7 }[/math]
[math]\displaystyle{ \alpha(d_1, \mathbf{1}00) \mapsto (1, E) }[/math]	x
[math]\displaystyle{ \alpha(d_1, \mathbf{0}00) \mapsto (0, d_2) }[/math]		x			x	x	x
[math]\displaystyle{ \alpha(d_1, 0\mathbf{1}0) \mapsto (1, E) }[/math]			x
[math]\displaystyle{ \alpha(d_1, 00\mathbf{1}) \mapsto (1, E) }[/math]				x
[math]\displaystyle{ \alpha(d_2, \mathbf{1}01) \mapsto (1, E) }[/math]		x
[math]\displaystyle{ \alpha(d_2, \mathbf{0}01) \mapsto (1, E) }[/math]						x
[math]\displaystyle{ \alpha(d_2, 0\mathbf{1}1) \mapsto (1, E) }[/math]					x
[math]\displaystyle{ \alpha(d_2, 11\mathbf{0}) \mapsto (0, E) }[/math]							x

Test cases are formed by tracing decision paths. For every decision [math]\displaystyle{ d_i;\ 0 \lt i \lt n+1 }[/math] a succeeding and preceding subpath is searched until every connected path has a start [math]\displaystyle{ S }[/math] and an end [math]\displaystyle{ E }[/math]: [math]\displaystyle{ \begin{align} T_1&=(d_1, 100) \vdash (1, E) \\ T_2&=(d_1, 000) \vdash (0, d_2, 100) \vdash (1, E) \\ T_3&=(d_1, 010) \vdash (1, E) \\ \vdots \\ T_{n+1} \end{align} }[/math]

Step 4: Physical test-case matrix

Table 4: Example Physical Test Cases

Factor\Test Case	[math]\displaystyle{ T_1 }[/math]	[math]\displaystyle{ T_2 }[/math]	[math]\displaystyle{ T_3 }[/math]	[math]\displaystyle{ T_4 }[/math]	[math]\displaystyle{ T_5 }[/math]	[math]\displaystyle{ T_6 }[/math]	[math]\displaystyle{ T_7 }[/math]
days	16	14			8	8	8
price			1100			600
departure							sa
member				silver
Result
0							0
-10		1			1	1
-20	1		1	1

Physical test cases are created from logical test cases by filling in actual value representations and their respective results.

Test-case graph

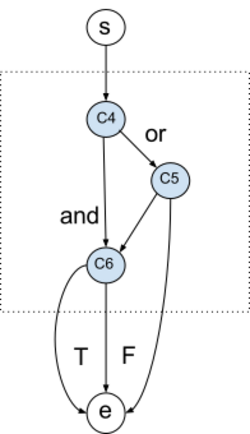
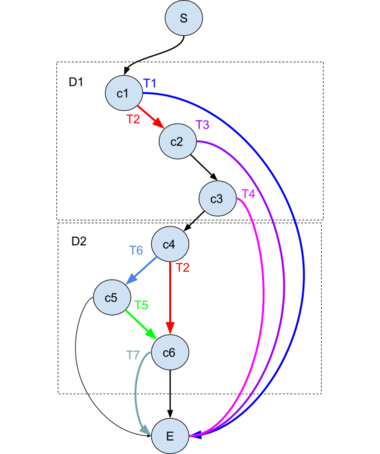
Figure 6: ECT Example Test Case Graph

In the example test case graph, all test cases and their isolated conditions are marked by colors, and the remaining paths are implicitly passed.

See also

• Code coverage § Multiple condition coverage
• Control-flow graph
• Decision-to-decision path