Irregularity of distributions
The irregularity of distributions problem, stated first by Hugo Steinhaus, is a numerical problem with a surprising result. The problem is to find N numbers, [math]\displaystyle{ x_1,\ldots,x_N }[/math], all between 0 and 1, for which the following conditions hold:
- The first two numbers must be in different halves (one less than 1/2, one greater than 1/2).
- The first 3 numbers must be in different thirds (one less than 1/3, one between 1/3 and 2/3, one greater than 2/3).
- The first 4 numbers must be in different fourths.
- The first 5 numbers must be in different fifths.
- etc.
Mathematically, we are looking for a sequence of real numbers
- [math]\displaystyle{ x_1,\ldots,x_N }[/math]
such that for every n ∈ {1, ..., N} and every k ∈ {1, ..., n} there is some i ∈ {1, ..., k} such that
- [math]\displaystyle{ \frac{k-1}{n} \leq x_i \lt \frac{k}{n}. }[/math]
Solution
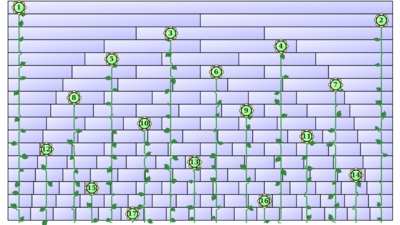
The surprising result is that there is a solution up to N = 17, but starting at N = 18 and above it is impossible. A possible solution for N ≤ 17 is shown diagrammatically on the right; numerically it is as follows:
- [math]\displaystyle{ \begin{align} x_{1} & = 0.029 \\ x_{2} & = 0.971 \\ x_{3} & = 0.423 \\ x_{4} & = 0.71 \\ x_{5} & = 0.27 \\ x_{6} & = 0.542 \\ x_{7} & = 0.852 \\ x_{8} & = 0.172 \\ x_{9} & = 0.62 \\ x_{10} & = 0.355 \\ x_{11} & = 0.777 \\ x_{12} & = 0.1 \\ x_{13} & = 0.485 \\ x_{14} & = 0.905 \\ x_{15} & = 0.218 \\ x_{16} & = 0.667 \\ x_{17} & = 0.324 \end{align} }[/math]
In this example, considering for instance the first 5 numbers, we have
- [math]\displaystyle{ 0 \lt x_1 \lt \frac{1}{5} \lt x_5 \lt \frac{2}{5} \lt x_3 \lt \frac{3}{5} \lt x_4 \lt \frac{4}{5} \lt x_2 \lt 1. }[/math]
Mieczysław Warmus concluded that 768 (1536, counting symmetric solutions separately) distinct sets of intervals satisfy the conditions for N = 17.
References
- H. Steinhaus, One hundred problems in elementary mathematics, Basic Books, New York, 1964, page 12
- Berlekamp, E. R.; Graham, R. L. (1970). "Irregularities in the distributions of finite sequences". Journal of Number Theory 2 (2): 152–161. doi:10.1016/0022-314X(70)90015-6. Bibcode: 1970JNT.....2..152B.
- M. Warmus, "A Supplementary Note on the Irregularities of Distributions", Journal of Number Theory 8, 260–263, 1976.
 |