Rocha–Thatte cycle detection algorithm
Rocha–Thatte algorithm[1] is a distributed algorithm in graph theory for detecting cycles on large-scale directed graphs based on the bulk synchronous message passing abstraction. This algorithm for detecting cycles by message passing is suitable to be implemented in distributed graph processing systems, and it is also suitable for implementations in systems for disk-based computations, such as the GraphChi,[2] where the computation is mainly based on secondary memory. Disk-based computations are necessary when we have a single computer for processing large-scale graphs, and the computation exceeds the primary memory capacity.
Overview
The Rocha–Thatte algorithm is a general algorithm for detecting cycles in a directed graph [math]\displaystyle{ G }[/math] by message passing among its vertices, based on the bulk synchronous message passing abstraction. This is a vertex-centric approach in which the vertices of the graph work together for detecting cycles. The bulk synchronous parallel model consists of a sequence of iterations, in each of which a vertex can receive messages sent by other vertices in the previous iteration, and send messages to other vertices.
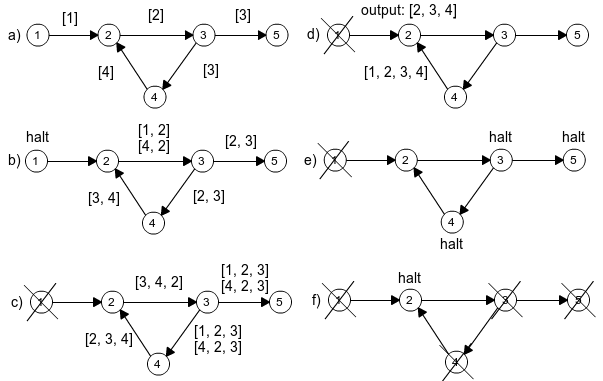
In each pass, each active vertex of [math]\displaystyle{ G }[/math] sends a set of sequences of vertices to its out-neighbours as described next. In the first pass, each vertex [math]\displaystyle{ v }[/math] sends the message [math]\displaystyle{ (v) }[/math] to all its out-neighbours. In subsequent iterations, each active vertex [math]\displaystyle{ v }[/math] appends [math]\displaystyle{ v }[/math] to each sequence it received in the previous iteration. It then sends all the updated sequences to its out-neighbours. If [math]\displaystyle{ v }[/math] has not received any message in the previous iteration, then [math]\displaystyle{ v }[/math] deactivates itself. The algorithm terminates when all the vertices have been deactivated.
For a sequence [math]\displaystyle{ (v_1, v_2, \ldots , v_k) }[/math] received by vertex [math]\displaystyle{ v }[/math], the appended sequence is not forwarded in two cases: (i) if [math]\displaystyle{ v = v_1 }[/math], then [math]\displaystyle{ v }[/math] has detected a cycle, which is reported; (ii) if [math]\displaystyle{ v = v_i }[/math] for some [math]\displaystyle{ i \in {2, 3, \ldots , k} }[/math], then [math]\displaystyle{ v }[/math] has detected a sequence that contains the cycle [math]\displaystyle{ (v = v_i, v_{i+1}, \ldots , v_k, v_{k+1} = v) }[/math]; in this case, the sequence is discarded, since the cycle must have been detected in an earlier iteration; to be precise, this cycle must have been detected in iteration [math]\displaystyle{ k - i + 1 }[/math]. Every cycle [math]\displaystyle{ (v_1, v_2, \ldots , v_k, v_{k+1} = v_1) }[/math] is detected by all [math]\displaystyle{ v_i, i = 1 }[/math] to [math]\displaystyle{ k }[/math] in the same iteration; it is reported by the vertex [math]\displaystyle{ \min\{v_1, \ldots , v_k\} }[/math].
The figure below presents an example of the execution of the algorithm. In iteration [math]\displaystyle{ i=3 }[/math], all the three vertices detect the cycle [math]\displaystyle{ (2, 3, 4) }[/math]. The algorithm ensures that the cycle is reported only once by emitting the detected cycle only from the vertex with the least identifier value in the ordered sequence, which is the vertex 2 in the example.[1]
The total number of iterations of the algorithm is the number of vertices in the longest path in the graph, plus a few more steps for deactivating the final vertices. During the analysis of the total number of iterations, we ignore the few extra iterations needed for deactivating the final vertices and detecting the end of the computation, since it is [math]\displaystyle{ O(1) }[/math] iterations. In practice, the actual number of these final few iterations depends on the framework being used to implement the algorithm.[1]
Experimental Performance
Simulations[3] show that the Rocha-Thatte algorithm has a smaller communication overhead than a distributed version of depth-first search, regarding both the number of messages and the total number of bits sent. Specifically, the distributed version of DFS may require up to one order of magnitude more messages exchanged than the Rocha-Thatte algorithm.
References
- ↑ 1.0 1.1 1.2 Rocha, Rodrigo Caetano; Thatte, Bhalchandra (2015), Distributed cycle detection in large-scale sparse graphs, Simpósio Brasileiro de Pesquisa Operacional (SBPO), doi:10.13140/RG.2.1.1233.8640
- ↑ Kyrola; Blelloch; Guestrin (2012), GraphChi: Large-scale graph computation on just a PC, http://dl.acm.org/citation.cfm?id=2387880.2387884
- ↑ Oliva, Gabriele; Setola, Roberto; Glielmo, Luigi; Hadjicostis, Christoforos (2016), "Distributed Cycle Detection and Removal", IEEE Transactions on Control of Network Systems 5: 194–204, doi:10.1109/TCNS.2016.2593264
 |