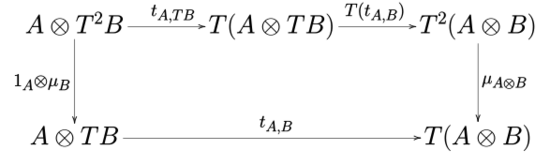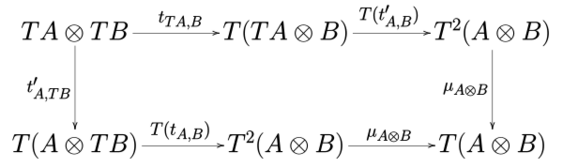Strong monad
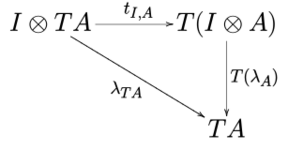
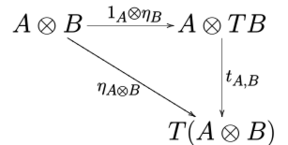
In category theory, a strong monad over a monoidal category (C, ⊗, I) is a monad (T, η, μ) together with a natural transformation tA,B : A ⊗ TB → T(A ⊗ B), called (tensorial) strength, such that the diagrams
commute for every object A, B and C (see Definition 3.2 in [1]).
If the monoidal category (C, ⊗, I) is closed then a strong monad is the same thing as a C-enriched monad.
Commutative strong monads
For every strong monad T on a symmetric monoidal category, a costrength natural transformation can be defined by
- [math]\displaystyle{ t'_{A,B}=T(\gamma_{B,A})\circ t_{B,A}\circ\gamma_{TA,B} : TA\otimes B\to T(A\otimes B) }[/math].
A strong monad T is said to be commutative when the diagram
commutes for all objects [math]\displaystyle{ A }[/math] and [math]\displaystyle{ B }[/math].[2]
One interesting fact about commutative strong monads is that they are "the same as" symmetric monoidal monads. More explicitly,
- a commutative strong monad [math]\displaystyle{ (T,\eta,\mu,t) }[/math] defines a symmetric monoidal monad [math]\displaystyle{ (T,\eta,\mu,m) }[/math] by
- [math]\displaystyle{ m_{A,B}=\mu_{A\otimes B}\circ Tt'_{A,B}\circ t_{TA,B}:TA\otimes TB\to T(A\otimes B) }[/math]
- and conversely a symmetric monoidal monad [math]\displaystyle{ (T,\eta,\mu,m) }[/math] defines a commutative strong monad [math]\displaystyle{ (T,\eta,\mu,t) }[/math] by
- [math]\displaystyle{ t_{A,B}=m_{A,B}\circ(\eta_A\otimes 1_{TB}):A\otimes TB\to T(A\otimes B) }[/math]
and the conversion between one and the other presentation is bijective.
References
- ↑ Moggi, Eugenio (July 1991). "Notions of computation and monads". Information and Computation 93 (1): 55–92. doi:10.1016/0890-5401(91)90052-4. http://www.disi.unige.it/person/MoggiE/ftp/ic91.pdf.
- ↑ Muscholl, Anca, ed (2014). Foundations of software science and computation structures : 17th (Aufl. 2014 ed.). [S.l.]: Springer. pp. 426–440. ISBN 978-3-642-54829-1.
- Anders Kock (1972). "Strong functors and monoidal monads". Archiv der Mathematik 23: 113–120. doi:10.1007/BF01304852. http://home.imf.au.dk/kock/SFMM.pdf.
- Jean Goubault-Larrecq, Slawomir Lasota and David Nowak (2005). "Logical Relations for Monadic Types". Mathematical Structures in Computer Science 18 (6): 1169. doi:10.1017/S0960129508007172.
 |