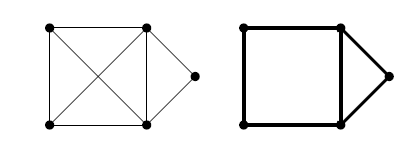
k-connectivity certificate

Graph on the right is a k-connectivity certificate for the graph G on the left for k=1,2.

In graph theory, for a k-connected graph G = (V, E), a subset of edges [math]\displaystyle{ E' \subseteq E }[/math] is considered a certificate for the k-connectivity of the graph G if and only if the subgraph G' = (V, E') is k-connected.

Sparse certificates

For a k-connected graph with n vertices, there always exists a k-connectivity certificate with at most k(n-1) edges. K-connectivity certificates are considered sparse if they contain O(kn) edges. In this figure, the graph on the right is also a sparse certificate for the graph G on the left.

Scan-first search

Scan-First is an algorithm for the parallel construction of k-connectivity certificates for graphs. It was introduced in the paper Scan-First Search and Sparse Certificates: An Improved Parallel Algorithm for K-Vertex Connectivity by Joseph Cheriyan, Ming-Yang Kao, and Ramakrishna Thurimella. The Scan-First Search algorithm improves the running time of building a sparse certificate for k-connectivity using the parallel computation model.

We can find a sparse certificate for k-connectivity by iteratively running scan-first search k times on sub-graphs of our input graph. Our input is a graph G = (V, E) and a root vertex r. For each iteration of scan-first search, we first compute a spanning tree T of our input graph G, and assign a pre-order numbering to all the vertices, which we will use as our scanning order. From our root r, we first scan r, which involves marking all its neighboring vertices.

Given a connected undirected graph and a specified vertex, a scan-first search in the graph starting from the specified vertex is a systematic way of marking the vertices. The main marking step is called scan: to scan a marked vertex means to mark all previously unmarked neighbors of that vertex. At the beginning of the search, only the specified starting vertex is marked. Then the search iteratively scans a marked and unscanned vertex until all vertices are scanned.

A scan-first search in a connected undirected graph produces a spanning tree defined as follows. At the beginning of the search, the tree is empty. Then, for each vertex x in the graph, when x is scanned, all the edges between x and its previously unmarked neighbors are added to the tree; the edges between x and its previously marked neighbors are not added to the tree.

An example showing two iterations of scan-first search on the graph G. For a k-Connected graph, we do k iterations of Scan-first Search. First and second iterations of Scan-first Search are shown above.

All previously unmarked vertices constitute the end-point of an edge from the currently scanned vertex, so if we start from some vertex v, and it has neighbors w and x, then if both w and x are unmarked, we create the edges (v, w) and (v, x) and add them to our output tree T'. If either w or x was previously marked, we do not add the edge that includes that vertex to T'. With these new edges in T', we move to the next vertex with the lowest preorder number to scan, which involves continuously marking previously unmarked vertices and adding the edges from the current vertex to these vertices to our output tree.

We use scan-first search to generate certificates for k-connectivity by running it for k iterations. An important note moving forward is that for each edge added to some output tree T' in each iteration, we remove the edges from the original graph G so they may not be included in some spanning forest for the next iteration. However, we can view the markings on the vertices as reset, so no vertices are marked on the next iteration.

Once we have exhausted all vertices, we have an edge set for the first iteration, E₁. We then remove E₁ from G = G₀, and make that G₁, and move onto the second iteration using the graph G₁. At the end of each iteration we have:

• • E_i : The set of edges we encountered during our scan-first search
  • F_i : Scan-first search forest, the grouping of edges into what may be separate trees at each step.
  • G_i : The resulting graph from removing E_i from the graph G_i-1 that we used to begin this iteration.
  • H_i : The union the edges from every iteration to now, E₁ ∪ E₂ ∪ ... ∪ E_i.

We say that H_k is the sparse certificate for the graph G.

The Main Certificate Theorem

Given an undirected graph G = (V, E) with n vertices, let k be some positive integer. For all i = 1, 2, . . . , k, let E_i be the set of edges generated by the i-th iteration of scan-first search, corresponding to a graph G_i−1 = (V, E − (E₁ ∪ . . . ∪ E_i−1)). So for each iteration of scan-first search, as stated above, we will remove edges from the graph G to create some new graph G_i that results at the end of the ith iteration. For every iteration i, our scan-first search forest is built from the graph G_i−1, where G = G₀. The claim of the Main Certificate Theorem is that the union E₁ ∪ . . . ∪ E_k is a certificate for the k-vertex connectivity of G and that it has at most k(n − 1) edges.

Computational complexity

The most important running-time is that of the algorithm running in parallel, using the CRCW PRAM model in this case. Our first spanning tree T can be found in O(log n) time using C(n,m) processors. Our preorder numbers and neighbours can also be calculated in O(log n) time because parallel techniques with O((n + m)/log n) processors, our C(n,m) value. For this reason, we can generate a single T&prime corresponding to one iteration in O(log n) time.

Using a distributed breadth-first search approach, we can find our spanning forest in O(d log³ n) time on a graph with diameter d using O(m + n log³ n) messages. The sequential approach is quite simply the running time for breadth-first search, O(m + n).

See also

• k-vertex connectivity
• k-edge connectivity
• Menger's theorem
• Connectivity (graph theory)