Butterfly curve (transcendental)
From HandWiki
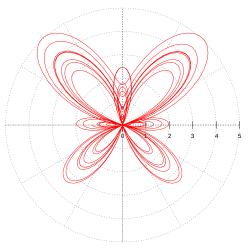
The butterfly curve is a transcendental plane curve discovered by Temple H. Fay of University of Southern Mississippi in 1989.[1]
Equation

An animated construction gives an idea of the complexity of the curve (Click for enlarged version).
The curve is given by the following parametric equations:[2]
- [math]\displaystyle{ x = \sin t \!\left(e^{\cos t} - 2\cos 4t - \sin^5\!\Big({t \over 12}\Big)\right) }[/math]
- [math]\displaystyle{ y = \cos t \!\left(e^{\cos t} - 2\cos 4t - \sin^5\!\Big({t \over 12}\Big)\right) }[/math]
- [math]\displaystyle{ 0 \le t \le 12\pi }[/math]
or by the following polar equation:
- [math]\displaystyle{ r = e^{\sin\theta} - 2\cos 4\theta + \sin^5\left(\frac{2\theta - \pi}{24}\right) }[/math]
The sin term has been added for purely aesthetic reasons, to make the butterfly appear fuller and more pleasing to the eye.[1]
Developments
In 2006, two mathematicians using Mathematica analyzed the function, and found variants where leaves, flowers or other insects became apparent.[3]
See also
https://books.google.com/books?id=AsYaCgAAQBAJ&dq=OSCAR+RAMIREZ+POLAR+EQUATION&pg=PA732
r = (cos 5θ)2 + sin 3θ + 0.3 for 0 ≤ θ ≤ 6π (A polar equation discovered by Oscar Ramirez, a UCLA student, in the fall of 1991.)
References
- ↑ 1.0 1.1 Fay, Temple H. (May 1989). "The Butterfly Curve". Amer. Math. Monthly 96 (5): 442–443. doi:10.2307/2325155.
- ↑ Weisstein, Eric W.. "Butterfly Curve". http://mathworld.wolfram.com/ButterflyCurve.html.
- ↑ Geum, Y.H.; Kim, Y.I. (June 2008). "On the analysis and construction of the butterfly curve using Mathematica". International Journal of Mathematical Education in Science and Technology 39 (5): 670–678. doi:10.1080/00207390801923240.
External links
 |