Hart circle

The circle H touches the incircles I, [math]\displaystyle{ I_A }[/math],[math]\displaystyle{ I_B }[/math],[math]\displaystyle{ I_C }[/math] of a circular triangle ABC and its associated triangles.

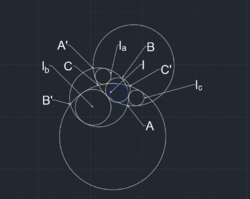
In geometry, the Hart circle is derived from three given circles that cross pairwise to form eight circular triangles. For any one of these eight triangles, and its three neighboring triangles, there exists a Hart circle, tangent to the inscribed circles of these four circular triangles. Thus, the three given circles have eight Hart circles associated with them. The Hart circles are named after their discover, Andrew Searle Hart. They can be seen as analogous to the nine-point circle of straight-sided triangles.

External links

• History of the Nine-Point Circle, Cambridge University
• Discussion of Hart Circle in context of Feuerbach's theorem
• On Centers and Central Lines of Triangles in the Elliptic Plane
• CRC Concise Encyclopedia of Mathematics by Eric W. Weisstein