Engineering:Reciprocity (electrical networks)

Reciprocity in electrical networks is a property of a circuit that relates voltages and currents at two points. The reciprocity theorem states that the current at one point in a circuit due to a voltage at a second point is the same as the current at the second point due to the same voltage at the first. The reciprocity theorem is valid for almost all passive networks. The reciprocity theorem is a feature of a more general principle of reciprocity in electromagnetism.

Description

If a current, [math]\displaystyle{ I_\text {A} }[/math], injected into port A produces a voltage, [math]\displaystyle{ V_\text {B} }[/math], at port B and [math]\displaystyle{ I_\text {A} }[/math] injected into port B produces [math]\displaystyle{ V_\text {B} }[/math] at port A, then the network is said to be reciprocal. Equivalently, reciprocity can be defined by the dual situation; applying voltage, [math]\displaystyle{ V_\text {A} }[/math], at port A producing current [math]\displaystyle{ I_\text {B} }[/math] at port B and [math]\displaystyle{ V_\text {A} }[/math] at port B producing current [math]\displaystyle{ I_\text {B} }[/math] at port A. In general, passive networks are reciprocal. Any network that consists entirely of ideal capacitances, inductances (including mutual inductances), and resistances, that is, elements that are linear and bilateral, will be reciprocal. However, passive components that are non-reciprocal do exist. Any component containing ferromagnetic material is likely to be non-reciprocal. Examples of passive components deliberately designed to be non-reciprocal include circulators and isolators.

The transfer function of a reciprocal network has the property that it is symmetrical about the main diagonal if expressed in terms of a z-parameter, y-parameter, or s-parameter matrix. A non-symmetrical matrix implies a non-reciprocal network. A symmetric matrix does not imply a symmetric network.

In some parametisations of networks, the representative matrix is not symmetrical for reciprocal networks. Common examples are h-parameters and ABCD-parameters, but they all have some other condition for reciprocity that can be calculated from the parameters. For h-parameters the condition is [math]\displaystyle{ h_{12} = - h_{21} }[/math] and for the ABCD parameters it is [math]\displaystyle{ AD - BC = 1 }[/math]. These representations mix voltages and currents in the same column vector and therefore do not even have matching units in transposed elements.

Example

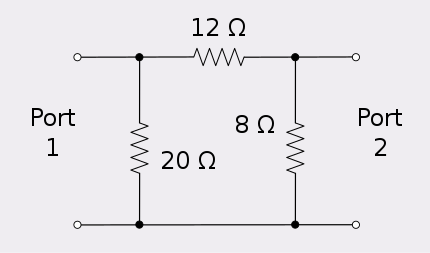
An example of reciprocity can be demonstrated using an asymmetrical resistive attenuator. An asymmetrical network is chosen as the example because a symmetrical network is self-evidently reciprocal.

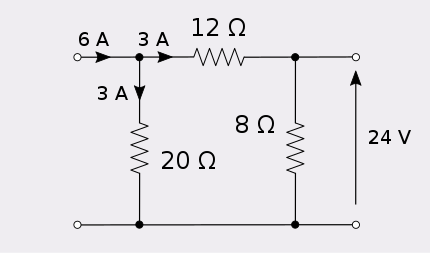
Injecting six amps into port 1 of this network produces 24 volts at port 2.

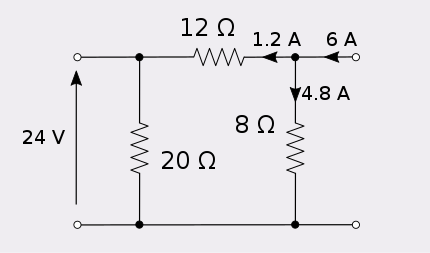
Injecting six amps into port 2 produces 24 volts at port 1.

Hence, the network is reciprocal. In this example, the port that is not injecting current is left open circuit. This is because a current generator applying zero current is an open circuit. If, on the other hand, one wished to apply voltages and measure the resulting current, then the port to which the voltage is not applied would be made short circuit. This is because a voltage generator applying zero volts is a short circuit.

Proof

Reciprocity of electrical networks is a special case of Lorentz reciprocity, but it can also be proven more directly from network theorems. This proof shows reciprocity for a two-node network in terms of its admittance matrix, and then shows reciprocity for a network with an arbitrary number of nodes by an induction argument. A linear network can be represented as a set of linear equations through nodal analysis. For a network consisting of n+1 nodes (one being a reference node) where, in general, an admittance is connected between each pair of nodes and where a current is injected in each node (provided by an ideal current source connected between the node and the reference node), these equations can be expressed in the form of an admittance matrix,

[math]\displaystyle{ \begin{bmatrix} I_1\\ I_2\\ \vdots\\ I_n \end{bmatrix}= \begin{bmatrix} Y_{11} & Y_{12} & \cdots & Y_{1n} \\ Y_{21} & Y_{22} & \cdots & Y_{2n} \\ \vdots & \vdots & \ddots & \vdots\\ Y_{n1} & Y_{n2} & \cdots & Y_{nn} \end{bmatrix} \begin{bmatrix} V_1\\ V_2\\ \vdots\\ V_n \end{bmatrix} }[/math]

where

[math]\displaystyle{ I_k }[/math] is the current injected into node k by a generator (which amounts to zero if no current source is connected to node k)

[math]\displaystyle{ V_k }[/math] is the voltage at node k with respect to the reference node (one could also say, it is the electric potential at node k)

[math]\displaystyle{ Y_{jk} }[/math] (j ≠ k) is the negative of the admittance directly connecting nodes j and k (if any)

[math]\displaystyle{ Y_{kk} }[/math] is the sum of the admittances connected to node k (regardless of the other node the admittance is connected to).

This representation corresponds to the one obtained by nodal analysis. If we further require that network is made up of passive, bilateral elements, then

[math]\displaystyle{ Y_{jk} = Y_{kj} }[/math]

since the admittance connected between nodes j and k is the same element as the admittance connected between nodes k and j. The matrix is therefore symmetrical. For the case where [math]\displaystyle{ n = 2 }[/math] the matrix reduces to,

[math]\displaystyle{ \begin{bmatrix} I_1 \\ I_2 \end{bmatrix}= \begin{bmatrix} Y_{11} & Y_{12} \\ Y_{21} & Y_{22} \end{bmatrix} \begin{bmatrix} V_1 \\ V_2 \end{bmatrix} }[/math].

From which it can be seen that,

[math]\displaystyle{ Y_{12} = \left . \frac {I_1}{V_2} \right |_{V_1=0} }[/math] and

[math]\displaystyle{ Y_{21} = \left . \frac {I_2}{V_1} \right |_{V_2=0} \ . }[/math]

But since [math]\displaystyle{ Y_{12} = Y_{21} }[/math] then,

[math]\displaystyle{ \left . \frac {I_1}{V_2} \right |_{V_1=0} = \left . \frac {I_2}{V_1} \right |_{V_2=0} }[/math]

which is synonymous with the condition for reciprocity. In words, the ratio of the current at one port to the voltage at another is the same ratio if the ports being driven and measured are interchanged. Thus reciprocity is proven for the case of [math]\displaystyle{ n = 2 }[/math].

For the case of a matrix of arbitrary size, the order of the matrix can be reduced through node elimination. After eliminating the sth node, the new admittance matrix will have the form,

[math]\displaystyle{ \begin{bmatrix} (Y_{11}Y_{ss} - Y_{s1}Y_{1s}) & (Y_{12}Y_{ss} - Y_{s2}Y_{1s}) & (Y_{13}Y_{ss} - Y_{s3}Y_{1s}) & \cdots \\ (Y_{21}Y_{ss} - Y_{s1}Y_{2s}) & (Y_{22}Y_{ss} - Y_{s2}Y_{2s}) & (Y_{23}Y_{ss} - Y_{s3}Y_{2s}) & \cdots \\ (Y_{31}Y_{ss} - Y_{s1}Y_{3s}) & (Y_{32}Y_{ss} - Y_{s2}Y_{3s}) & (Y_{33}Y_{ss} - Y_{s3}Y_{3s}) & \cdots \\ \cdots & \cdots & \cdots & \cdots \end{bmatrix} }[/math]

It can be seen that this new matrix is also symmetrical. Nodes can continue to be eliminated in this way until only a 2×2 symmetrical matrix remains involving the two nodes of interest. Since this matrix is symmetrical it is proved that reciprocity applies to a matrix of arbitrary size when one node is driven by a voltage and current measured at another. A similar process using the impedance matrix from mesh analysis demonstrates reciprocity where one node is driven by a current and voltage is measured at another.

Bibliography

• Bakshi, U.A.; Bakshi, A.V., Electrical Networks, Technical Publications, 2008 ISBN:8184314647.
• Guillemin, Ernst A., Introductory Circuit Theory, New York: John Wiley & Sons, 1953 OCLC 535111
• Kumar, K. S. Suresh, Electric Circuits and Networks, Pearson Education India, 2008 ISBN:8131713903.
• Harris, Vincent G., "Microwave ferrites and applications", ch. 14 in, Mailadil T. Sebastian, Rick Ubic, Heli Jantunen, Microwave Materials and Applications, John Wiley & Sons, 2017 ISBN:1119208521.
• Zhang, Kequian; Li, Dejie, Electromagnetic Theory for Microwaves and Optoelectronics, Springer Science & Business Media, 2013 ISBN:3662035537.