Engineering:Reciprocity (optoelectronic)
Optoelectronic reciprocity relations relate properties of a diode under illumination to the photon emission of the same diode under applied voltage. The relations are useful for interpretation of luminescence based measurements of solar cells and modules and for the analysis of recombination losses in solar cells.
Basics
Solar cells and light-emitting diodes are both semiconducting diodes that are operated in a different voltage and illumination regime and that serve different purposes. A solar cell is operated under illumination (usually by solar radiation) and is typically kept at the maximum power point where the product of current and voltage are maximized. A light emitting diode is operated at an applied forward bias (without external illumination). While a solar cell converts the energy contained in the electromagnetic waves of the incoming solar radiation into electric power (voltage x current) a light-emitting diode does the inverse, namely converting electrical power into electromagnetic radiation. A solar cell and a light emitting diode are typically made from different materials and optimized for different purposes; however, conceptually every solar cell could be operated as a light emitting diode and vice versa. Given that the operation principles have a high symmetry it is fair to assume that the key figures of merit that are used to characterize photovoltaic and luminescent operation of diodes are related to each other. These relations become particularly simple in a situation, where recombination rates scale linearly with minority carrier density and are explained below.
Reciprocity between the photovoltaic quantum efficiency and the electroluminescence spectrum of a pn-junction diode
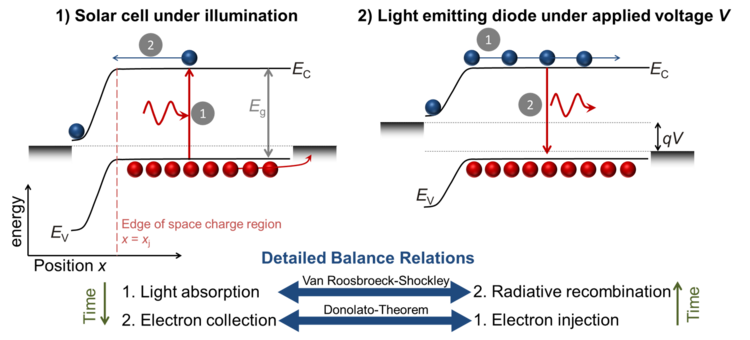
The photovoltaic quantum efficiency [math]\displaystyle{ Q_{e,PV} }[/math] is a spectral quantity that is generally measured as a function of photon energy (or wavelength). The same is true for the electroluminescence spectrum [math]\displaystyle{ \phi_{EL} }[/math] of a light emitting diode under applied forward voltage [math]\displaystyle{ V }[/math]. Under certain conditions specified below, these two properties measured on the same diode are connected via the equation[1]
- [math]\displaystyle{ \phi_{EL}=Q_{e,PV}\phi_{bb}[\exp{\frac{qV}{kT}}-1] }[/math] (1)
where [math]\displaystyle{ \phi_{bb} }[/math] is the black body spectrum emitted by a surface (the diode) into the hemisphere above the diode in units of photons per area, time and electron interval. In this case the black body spectrum is given by
- [math]\displaystyle{ \phi_{bb}=\frac{2\pi}{h^3c^2}\frac{E^2}{\exp{E/kT}-1} }[/math]
where [math]\displaystyle{ k }[/math] is the Boltzmann constant, [math]\displaystyle{ h }[/math] is Planck's constant, [math]\displaystyle{ c }[/math] is the speed of light in vacuum, and [math]\displaystyle{ T }[/math] is the temperature of the diode. This simple relation is useful for the analysis of solar cells using luminescence-based characterization methods. Luminescence used for characterization of solar cells is useful because of the ability to image the luminescence of solar cells and modules in short periods of times, while spatially resolved measurements of photovoltaic properties (such as photocurrent or photovoltage) would be very time-consuming and technically difficult.
Equation (1) is valid for the practically relevant situation, where the neutral base region of a pn-junction makes up most of the volume of the diode. Typically, the thickness of a crystalline Si solar cell is ~ 200 µm while the thickness of the emitter and space charge region is only on the order of hundreds of nanometers, i.e. three orders of magnitude thinner. In the base of a pn-junction, recombination is typically linear with minority carrier concentration over a large range of injection conditions and charge carrier transport is by diffusion. In this situation, the Donolato theorem.[2] is valid that states that the collection efficiency [math]\displaystyle{ f_c }[/math] is related to the normalized minority carrier concentration [math]\displaystyle{ \delta n(x)/\delta n(x=x_j) }[/math] via
- [math]\displaystyle{ f_c(x)=\frac{\delta n(x)}{\delta n(x=x_j)} }[/math]
where [math]\displaystyle{ x }[/math] is a spatial coordinate and [math]\displaystyle{ x_j }[/math] defines the position of the edge of the space charge region (where the neutral zone and the space charge region connect). Thus, if [math]\displaystyle{ x=x_j }[/math], the collection efficiency is one. Further away from the edge of the space charge region, the collection efficiency will be smaller than one depending on the distance and the amount of recombination happening in the neutral zone. The same holds for the electron concentration in the dark under applied bias. Here, the electron concentration will also decrease from the edge of the space charge region towards the back contact. This decrease as well as the collection efficiency will be approximately exponential (with the diffusion length controlling the decay).
The Donolato theorem is based on the principle of detailed balance and connects the processes of charge carrier injection (relevant in the luminescent mode of operation) and charge carrier extraction (relevant in the photovoltaic mode of operation). In addition, the detailed balance between absorption of photons and radiative recombination can be mathematically expressed using the van Roosbroeck-Shockley[3] equation as
- [math]\displaystyle{ k_{rad}n_i^2=\int\alpha4n_r^2\phi_{bb}dE }[/math]
Here, [math]\displaystyle{ \alpha }[/math] is the absorption coefficient, [math]\displaystyle{ k_{rad} }[/math] is the radiative recombination coefficient, [math]\displaystyle{ n_r }[/math] is the refractive index, [math]\displaystyle{ n_i }[/math] is the intrinsic charge carrier concentration. A derivation of equation (1) can be found in ref.[1]
The reciprocity relation (eq. (1)) is only valid if absorption and emission is dominated by the neutral region of the pn-junction shown in the adjacent figure.[4] This is a good approximation for crystalline silicon solar cells and the method can also be used for copper indium gallium selenide solar cells. However the equations has limitations when applied to solar cells where the space charge region is of comparable size to the total absorber volume. This is the case for instance for organic solar cells or amorphous Si solar cells.[5] The reciprocity relation is also invalid if the emission of the solar cell is not from delocalized conduction and valence band states as would be the case for most mono and polycrystalline semiconductors but from localized states (defect states). This limitation is relevant for microcrystalline and amorphous silicon solar cells. [6]
Reciprocity between the open-circuit voltage of a solar cell and the external luminescence quantum efficiency
The open-circuit voltage [math]\displaystyle{ V_{oc} }[/math] of a solar cell is the voltage created by a certain amount of illumination if the contacts of the solar cell are not connected, i.e. in open circuit. The voltage that can build up in such as situation is directly connected to the density of electrons and holes in the device. These densities in turn depend on the rates of photogeneration (determined by the amount of illumination) and the rates of recombination. The rate of photogeneration is usually determined by the typically used illumination with white light with a power density of 100 mW/cm2 (called one sun) and by the band gap of the solar cell and does not change much between different devices of the same type. The rate of recombination however might vary over orders of magnitude depending on the quality of the material and the interfaces. Thus, the open-circuit voltage depends quite drastically on the rates of recombination at a given concentration of charge carriers. The highest possible open-circuit voltage, the radiative open-circuit voltage [math]\displaystyle{ V_{oc,rad} }[/math], is obtained if all recombination is radiative and non-radiative recombination is negligible. This is the ideal situation, because radiative recombination cannot be avoided other than by avoiding light absorption (principle of detailed balance). However, since absorption is a key requirement for a solar cell and necessary to achieve a high concentration of electrons and holes as well, radiative recombination is a necessity (see van Roosbroeck-Shockley equation [3]). If non-radiative recombination is substantial and non negligible, the open-circuit voltage will be reduced depending on the ratio between the radiative and non-radiative recombination currents (where the recombination currents are the integral of the recombination rates over volume). This leads to a second reciprocity relation between the photovoltaic and the luminescent operation mode of a solar cell because the ratio of radiative to total (radiative and non-radiative) recombination currents is the external luminescence quantum efficiency [math]\displaystyle{ Q_{e,lum} }[/math] of a (light emitting) diode. Mathematically, this relation is expressed as,[7][1]
- [math]\displaystyle{ qV_{oc,rad}-qV_{oc}=-kT\ln{Q_{e,lum}} (2) }[/math]
Thus, any reduction in the external luminescence quantum efficiency by one order of magnitude would lead to a reduction in open-circuit voltage (relative to [math]\displaystyle{ V_{oc,rad} }[/math]) by [math]\displaystyle{ kT/q\times \ln(10)\approx 60 mV }[/math]. Equation (2) is frequently used in the literature on solar cells. For instance for an improved understanding of the open-circuit voltage in organic solar cells[8] and for comparing voltage losses between different photovoltaic technologies.[9][10]
References
- ↑ 1.0 1.1 1.2 Rau, U. (2007). "Reciprocity relation between photovoltaic quantum efficiency and electroluminescent emission of solar cells". Physical Review B 76 (8): 085303. doi:10.1103/physrevb.76.085303. Bibcode: 2007PhRvB..76h5303R. http://juser.fz-juelich.de/search?p=id:%22PreJuSER-59297%22.
- ↑ Donolato, C. (1985). "A reciprocity theorem for charge collection". Applied Physics Letters 46 (3): 270–272. doi:10.1063/1.95654. Bibcode: 1985ApPhL..46..270D.
- ↑ 3.0 3.1 van Roosbroeck, W.; Shockley, W. (1954). "Photon-radiative recombination of electrons and holes in germanium". Physical Review 94 (6): 1558–1560. doi:10.1103/physrev.94.1558. Bibcode: 1954PhRv...94.1558V.
- ↑ Wang, X.; Lundstrom, M. S. (2013). "On the Use of Rau's Reciprocity to Deduce External Radiative Efficiency in Solar Cells". IEEE Journal of Photovoltaics 3 (4): 1348–1353. doi:10.1109/jphotov.2013.2278658. https://docs.lib.purdue.edu/ecepubs/112.
- ↑ Kirchartz, T.; Nelson, J.; Rau, U. (2016). "Reciprocity between charge injection and extraction and its influence on the interpretation of electroluminescence spectra in organic solar cells". Physical Review Applied 5 (5): 054003. doi:10.1103/physrevapplied.5.054003. Bibcode: 2016PhRvP...5e4003K.
- ↑ Müller, T. C. M.; Pieters, B. E.; Kirchartz, T.; Carius, R.; Rau, U. (2014). "Effect of localized states on the reciprocity between quantum efficiency and electroluminescence in Cu(In,Ga)Se2 and Si thin-film solar cells". Solar Energy Materials and Solar Cells 129: 95–103. doi:10.1016/j.solmat.2014.04.018.
- ↑ Ross, R. T. (1967). "Some thermodynamics of photochemical systems". J. Chem. Phys. 46 (12): 4590–4593. doi:10.1063/1.1840606. Bibcode: 1967JChPh..46.4590R. http://www.escholarship.org/uc/item/2586s34h.
- ↑ Vandewal, K.; Tvingstedt, K.; Gadisa, A.; Inganas, O.; Manca, J. V. (2009). "On the origin of the open-circuit voltage of polymer-fullerene solar cells". Nature Materials 8 (11): 904–9. doi:10.1038/nmat2548. PMID 19820700. Bibcode: 2009NatMa...8..904V.
- ↑ Green, M. A. (2012). "Radiative efficiency of state-of-the-art photovoltaic cells". Prog. Photovolt. 20 (4): 472–476. doi:10.1002/pip.1147.
- ↑ Rau, U.; Blank, B.; Müller, T. C. M.; Kirchartz, T. (2017). "Efficiency potential of photovoltaic materials and devices unveiled by detailed-balance analysis". Physical Review Applied 7 (4): 044016. doi:10.1103/physrevapplied.7.044016. Bibcode: 2017PhRvP...7d4016R.
 |

