Physics:Relative permeability

From HandWiki
Revision as of 03:31, 5 February 2024 by Pchauhan2001 (talk | contribs) (url)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: Dimensionless measure of a porous material's permeability


In multiphase flow in porous media, the relative permeability of a phase is a dimensionless measure of the effective permeability of that phase. It is the ratio of the effective permeability of that phase to the absolute permeability. It can be viewed as an adaptation of Darcy's law to multiphase flow.

For two-phase flow in porous media given steady-state conditions, we can write

[math]\displaystyle{ q_i = -\frac{k_i}{\mu_i} \nabla P_i \qquad \text{for} \quad i=1,2 }[/math]

where [math]\displaystyle{ q_i }[/math] is the flux, [math]\displaystyle{ \nabla P_i }[/math] is the pressure drop, [math]\displaystyle{ \mu_i }[/math] is the viscosity. The subscript [math]\displaystyle{ i }[/math] indicates that the parameters are for phase [math]\displaystyle{ i }[/math].

[math]\displaystyle{ k_i }[/math] is here the phase permeability (i.e., the effective permeability of phase [math]\displaystyle{ i }[/math]), as observed through the equation above.

Relative permeability, [math]\displaystyle{ k_{\mathit{ri}} }[/math], for phase [math]\displaystyle{ i }[/math] is then defined from [math]\displaystyle{ k_i = k_{\mathit{ri}}k }[/math], as

[math]\displaystyle{ k_{\mathit{ri}} = k_i / k }[/math]

where [math]\displaystyle{ k }[/math] is the permeability of the porous medium in single-phase flow, i.e., the absolute permeability. Relative permeability must be between zero and one.

In applications, relative permeability is often represented as a function of water saturation; however, owing to capillary hysteresis one often resorts to a function or curve measured under drainage and another measured under imbibition.

Under this approach, the flow of each phase is inhibited by the presence of the other phases. Thus the sum of relative permeabilities over all phases is less than 1. However, apparent relative permeabilities larger than 1 have been obtained since the Darcean approach disregards the viscous coupling effects derived from momentum transfer between the phases (see assumptions below). This coupling could enhance the flow instead of inhibit it. This has been observed in heavy oil petroleum reservoirs when the gas phase flows as bubbles or patches (disconnected). [1]

Modelling assumptions

The above form for Darcy's law is sometimes also called Darcy's extended law, formulated for horizontal, one-dimensional, immiscible multiphase flow in homogeneous and isotropic porous media. The interactions between the fluids are neglected, so this model assumes that the solid porous media and the other fluids form a new porous matrix through which a phase can flow, implying that the fluid-fluid interfaces remain static in steady-state flow, which is not true, but this approximation has proven useful anyway.

Each of the phase saturations must be larger than the irreducible saturation, and each phase is assumed continuous within the porous medium.

Based on data from special core analysis laboratory (SCAL) experiments,[2] simplified models of relative permeability as a function of saturation (e.g. water saturation) can be constructed. This article will focus on an oil-water system.

Saturation scaling

Water saturation [math]\displaystyle{ S_\mathit{w} }[/math] is the fraction of porevolume that is filled with water, and similar for oil saturation [math]\displaystyle{ S_\mathit{o} }[/math]. Thus, saturations are in itselves scaled properties or variables. This gives the constraint

[math]\displaystyle{ S_\mathit{w} + S_\mathit{o} = 1 \Leftrightarrow S_\mathit{w} = 1 - S_\mathit{o} }[/math]

The model functions or correlations for relative permeabilities in an oil-water system are therefore usually written as functions of only water saturation, and this makes it natural to select water saturation as the horizontal axis in graphical presentations. Let [math]\displaystyle{ S_\mathit{wir} }[/math] (also denoted [math]\displaystyle{ S_\mathit{wc} }[/math] and sometimes [math]\displaystyle{ S_\mathit{wr} }[/math]) be the irreducible (or minimal or connate) water saturation, and let [math]\displaystyle{ S_\mathit{orw} }[/math] be the residual (minimal) oil saturation after water flooding (imbibition). The flowing water saturation window in a water invasion / injection / imbibition process is bounded by a minimum value [math]\displaystyle{ S_\mathit{wir} }[/math] and a maximum value [math]\displaystyle{ S_\mathit{wor} = 1 - S_\mathit{orw} }[/math]. In mathematical terms the flowing saturation window is written as

[math]\displaystyle{ S_\mathit{wir} \leq S_\mathit{w} \leq S_\mathit{wor} = 1 - S_\mathit{orw} }[/math]
Normalization of water saturation values

By scaling the water saturation to the flowing saturation window, we get a (new or another) normalized water saturation value

[math]\displaystyle{ S_\mathit{wn} = S_\mathit{wn}(S_w) = \frac{S_w - S_\mathit{wir}}{1-S_\mathit{wir} - S_\mathit{orw}} = \frac{S_w - S_\mathit{wir}}{S_\mathit{wor} - S_\mathit{wir}} }[/math]

and a normalized oil saturation value

[math]\displaystyle{ S_\mathit{on} = 1-S_\mathit{wn} = \frac{S_o - S_\mathit{orw}}{1-S_\mathit{wir} - S_\mathit{orw}} }[/math]

Endpoints

Let [math]\displaystyle{ K_\mathit{row} }[/math] be oil relative permeability, and let [math]\displaystyle{ K_\mathit{rw} }[/math] be water relative permeability. There are two ways of scaling phase permeability (i.e. effective permeability of the phase). If we scale phase permeability w.r.t. absolute water permeability (i.e. [math]\displaystyle{ S_\mathit{w} = 1 }[/math]), we get an endpoint parameter for both oil and water relative permeability. If we scale phase permeability w.r.t. oil permeability with irreducible water saturation present, [math]\displaystyle{ K_\mathit{row} }[/math] endpoint is one, and we are left with only the [math]\displaystyle{ K_\mathit{rw} }[/math] endpoint parameter. In order to satisfy both options in the mathematical model, it is common to use two endpoint symbols in the model for two-phase relative permeability. The endpoints / endpoint parameters of oil and water relative permeabilities are

[math]\displaystyle{ \begin{align} K_\mathit{row}(S_\mathit{wir}) = K_\mathit{rot} && \text{and} && K_\mathit{rw}(S_\mathit{wor}) = K_\mathit{rwr} \end{align} }[/math]

These symbols have their merits and limits. The symbol [math]\displaystyle{ K_\mathit{rot} }[/math] emphasize that it represents the top point of [math]\displaystyle{ K_\mathit{row} }[/math]. It occurs at irreducible water saturation, and it is the largest value of [math]\displaystyle{ K_\mathit{row} }[/math] that can occur for initial water saturation. The competing endpoint symbol [math]\displaystyle{ K_\mathit{ror} }[/math] occurs in imbibition flow in oil-gas systems. If the permeability basis is oil with irreducible water present, then [math]\displaystyle{ K_\mathit{rot} = 1 }[/math]. The symbol [math]\displaystyle{ K_\mathit{rwr} }[/math] emphasizes that it is occurring at the residual oil saturation. An alternative symbol to [math]\displaystyle{ K_\mathit{rwr} }[/math] is [math]\displaystyle{ K_\mathit{rw}^o }[/math] which emphasizes that the reference permeability is oil permeability with irreducible water [math]\displaystyle{ S_\mathit{wir} }[/math] present.

The oil and water relative permeability models are then written as

[math]\displaystyle{ \begin{align} K_\mathit{row} = K_\mathit{rot} \cdot K_\mathit{rown}(S_\mathit{wn}) && \text{and} && K_\mathit{rw} = K_\mathit{rwr} \cdot K_\mathit{rwn}(S_\mathit{wn}) \end{align} }[/math]

The functions [math]\displaystyle{ K_\mathit{rown} }[/math] and [math]\displaystyle{ K_\mathit{rwn} }[/math] are called normalised relative permeabilities or shape functions for oil and water, respectively. The endpoint parameters [math]\displaystyle{ K_\mathit{rot} }[/math] and [math]\displaystyle{ K_\mathit{rwr} }[/math] (which is a simplification of [math]\displaystyle{ K_\mathit{rwor} }[/math]) are physical properties that are obtained either before or together with the optimization of shape parameters present in the shape functions.

There are often many symbols in articles that discuss relative permeability models and modelling. A number of busy core analysts, reservoir engineers and scientists often skip using tedious and time-consuming subscripts, and write e.g. Krow instead of [math]\displaystyle{ K_\mathit{row} }[/math] or [math]\displaystyle{ k_\mathit{row} }[/math] or krow or oil relative permeability. A variety of symbols are therefore to be expected, and accepted as long as they are explained or defined.

The effects that slip or no-slip boundary conditions in pore flow have on endpoint parameters, are discussed by Berg et alios.[3][4]

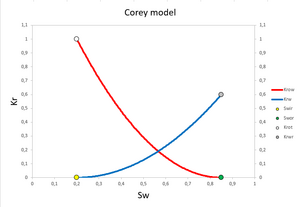
Corey-model

An often used approximation of relative permeability is the Corey correlation [5] [6] [7] which is a power law in saturation. The Corey correlations of the relative permeability for oil and water are then

Example of Corey-correlation for imbibition flow with [math]\displaystyle{ N_\mathit{o} }[/math] = [math]\displaystyle{ N_\mathit{w} = 2 }[/math] and [math]\displaystyle{ K_\mathit{rwr} = 0.6 }[/math].
[math]\displaystyle{ K_\mathit{row}(S_{w}) = K{_\mathit{rot}}(1-S_\mathit{wn})^{N_\mathit{o}} }[/math]
[math]\displaystyle{ K_\mathit{rw}(S_{w}) = K{_\mathit{rwr}}S_\mathit{wn}^{N_\mathit{w}} }[/math]

If the permeability basis is normal oil with irreducible water present, then [math]\displaystyle{ K_\mathit{rot} = 1 }[/math].

The empirical parameters [math]\displaystyle{ N_\mathit{o} }[/math] and [math]\displaystyle{ N_\mathit{w} }[/math] are called curve shape parameters or simply shape parameters, and they can be obtained from measured data either by analytical interpretation of measured data, or by optimization using a core flow numerical simulator to match the experiment (often called history matching). [math]\displaystyle{ N_\mathit{o} = N_\mathit{w} = 2 }[/math] is sometimes appropriate. The physical properties [math]\displaystyle{ K_\mathit{rot} }[/math] and [math]\displaystyle{ K_\mathit{rwr} }[/math] are obtained either before or together with the optimizing of [math]\displaystyle{ N_\mathit{o} }[/math] and [math]\displaystyle{ N_\mathit{w} }[/math].

In case of gas-water system or gas-oil system there are Corey correlations similar to the oil-water relative permeabilities correlations shown above.

LET-model

The Corey-correlation or Corey model has only one degree of freedom for the shape of each relative permeability curve, the shape parameter N. The LET-correlation[8] [9] adds more degrees of freedom in order to accommodate the shape of relative permeability curves in SCAL experiments[2] and in 3D reservoir models that are adjusted to match historic production. These adjustments frequently includes relative permeability curves and endpoints.

Example of LET-correlation for imbibition flow with L,E,T all equal to 2 and [math]\displaystyle{ K_\mathit{rwr} = 0.6 }[/math].

The LET-type approximation is described by 3 parameters L, E, T. The correlation for water and oil relative permeability with water injection is thus

[math]\displaystyle{ K_\mathit{rw}=\frac{{K_\mathit{rwr}}S_\mathit{wn}^{L_\mathit{w}}}{{S_\mathit{wn}}^{L_\mathit{w}}+{E_\mathit{w}}{(1-S_\mathit{wn})}^{T_\mathit{w}}} }[/math]

and

[math]\displaystyle{ K_\mathit{row}=\frac{K_\mathit{rot}(1-S_\mathit{wn})^{L_o}}{{(1-S_\mathit{wn})^{L_o}}+{E_\mathit{o}}S_\mathit{wn}^{T_\mathit{o}}} }[/math]

written using the same [math]\displaystyle{ S_w }[/math] normalization as for Corey.

Only [math]\displaystyle{ S_\mathit{wir} }[/math], [math]\displaystyle{ S_\mathit{orw} }[/math], [math]\displaystyle{ K_\mathit{rot} }[/math], and [math]\displaystyle{ K_\mathit{rwr} }[/math] have direct physical meaning, while the parameters L, E and T are empirical. The parameter L describes the lower part of the curve, and by similarity and experience the L-values are comparable to the appropriate Corey parameter. The parameter T describes the upper part (or the top part) of the curve in a similar way that the L-parameter describes the lower part of the curve. The parameter E describes the position of the slope (or the elevation) of the curve. A value of one is a neutral value, and the position of the slope is governed by the L- and T-parameters. Increasing the value of the E-parameter pushes the slope towards the high end of the curve. Decreasing the value of the E-parameter pushes the slope towards the lower end of the curve. Experience using the LET correlation indicates the following reasonable ranges for the parameters L, E, and T: L ≥ 0.1, E > 0 and T ≥ 0.1.

In case of gas-water system or gas-oil system there are LET correlations similar to the oil-water relative permeabilities correlations shown above.

Evaluations

After Morris Muskat et alios established the concept of relative permeability in late 1930'ies, the number of correlations, i.e. models, for relative permeability has steadily increased. This creates a need for evaluation of the most common correlations at the current time. Two of the latest (per 2019) and most thorough evaluations are done by Moghadasi et alios[10] and by Sakhaei et alios.[11] Moghadasi et alios[10] evaluated Corey, Chierici and LET correlations for oil/water relative permeability using a sophisticated method that takes into account the number of uncertain model parameters. They found that LET, with the largest number (three) of uncertain parameters, was clearly the best one for both oil and water relative permeability. Sakhaei et alios[11] evaluated 10 common and widely used relative permeability correlations for gas/oil and gas/condensate systems, and found that LET showed best agreement with experimental values for both gas and oil/condensate relative permeability.

See also

References

  1. ↑ Bravo, M.C.; Araujo, M. (2008). "Analysis of the Unconventional Behavior of Oil Relative Permeability during Depletion Tests of Gas-Saturated Heavy Oils". International Journal of Multiphase Flow 34 (5): 447–460. doi:10.1016/j.ijmultiphaseflow.2007.11.003. 
  2. ↑ 2.0 2.1 McPhee, C.; Reed, J.; Zubizarreta, I. (2015). Core Analysis: A Best Practice Guide. Elsevier. ISBN 978-0-444-63533-4. 
  3. ↑ Berg, S.; Cense, A.W.; Hofman, J.P.; Smits, R.M.M. (2007). "Flow in Porous Media with Slip Boundary Condition". Paper SCA2007-13 Presented at the 2007 International Symposium of the SCA, Calgary, Canada, 10 - 12 September, 2007. 
  4. ↑ Berg, S.; Cense, A.W.; Hofman, J.P.; Smits, R.M.M. (2008). "Two-Phase Flow in Porous Media with Slip Boundary Condition". Transport in Porous Media 74 (3): 275–292. doi:10.1007/s11242-007-9194-4. 
  5. ↑ Goda, H.M.; Behrenbruch, P. (2004). Using a Modified Brooks-Corey Model to Study Oil-Water Relative Permeability for Diverse Pore Structures. doi:10.2118/88538-MS. ISBN 978-1-55563-979-2. 
  6. ↑ Brooks, R.H.; Corey, A.T. (1964). "Hydraulic properties of porous media". Hydrological Papers 3. 
  7. ↑ Corey, A.T. (Nov 1954). "The Interrelation Between Gas and Oil Relative Permeabilities". Prod. Monthly 19 (1): 38–41. 
  8. ↑ Lomeland, F.; Ebeltoft, E.; Thomas, W.H. (2005). "A New Versatile Relative Permeability Correlation". Proceedings of the 2005 International Symposium of the SCA, Abu Dhabi, United Arab Emirates, October 31 - November 2, 2005. https://frode54.files.wordpress.com/2018/03/sca2005-32-kr-lomeland-et-al.pdf. 
  9. ↑ Lomeland, F. (2018). "Overview of the LET Family of Versatile Correlations for Flow Functions". Proceedings of the 2018 International Symposium of the SCA, Trondheim, Norway, 27 - 30 August, 2018. https://frode54.files.wordpress.com/2018/09/sca2018-056-overview-and-pc-h-pc-s-lomeland.pdf. 
  10. ↑ 10.0 10.1 Moghadasi, L.; Guadagnini, A.; Inzoli, F.; Bartosek, M. (2015). "Interpretation of two-phase relative permeability curves through multiple formulations and model quality criteria". Journal of Petroleum Science and Engineering 135: 738–749. doi:10.1016/j.petrol.2015.10.027. 
  11. ↑ 11.0 11.1 Sakhaei, Z.; Azin, R.; Osfouri, S. (2016). "Assessment of empirical/theoretical relative permeability correlations for gas-oil/condensate systems". Paper Presented at the 1st Persian Gulf Oil, Gas and Petrochemical Biennal Conference Held at the Persian Gulf University in, Bushehr, Iran, 20 April, 2016. 

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Relative_permeability&oldid=3278451"