Physics:Arago spot
File:Formation of the Arago spot.webm
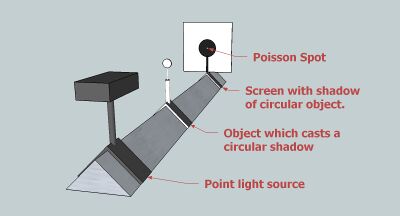
In optics, the Arago spot, Poisson spot,[1][2] or Fresnel spot[3] is a bright point that appears at the center of a circular object's shadow due to Fresnel diffraction.[4][5][6][7] This spot played an important role in the discovery of the wave nature of light and is a common way to demonstrate that light behaves as a wave.
The basic experimental setup requires a point source, such as an illuminated pinhole or a diverging laser beam. The dimensions of the setup must comply with the requirements for Fresnel diffraction. Namely, the Fresnel number must satisfy [math]\displaystyle{ F = \frac{d^2}{\ell \lambda} \gtrsim 1, }[/math] where
- d is the diameter of the circular object,
- ℓ is the distance between the object and the screen, and
- λ is the wavelength of the source.
Finally, the edge of the circular object must be sufficiently smooth.
These conditions together explain why the bright spot is not encountered in everyday life. However, with the laser sources available today, it is undemanding to perform an Arago-spot experiment.[8]
In astronomy, the Arago spot can also be observed in the strongly defocussed image of a star in a Newtonian telescope. There, the star provides an almost ideal point source at infinity, and the secondary mirror of the telescope constitutes the circular obstacle.
When light shines on the circular obstacle, Huygens' principle says that every point in the plane of the obstacle acts as a new point source of light. The light coming from points on the circumference of the obstacle and going to the center of the shadow travels exactly the same distance, so all the light passing close by the object arrives at the screen in phase and constructively interferes. This results in a bright spot at the shadow's center, where geometrical optics and particle theories of light predict that there should be no light at all.
History
At the beginning of the 19th century, the idea that light does not simply propagate along straight lines gained traction. Thomas Young published his double-slit experiment in 1807.[9] The original Arago spot experiment was carried out a decade later and was the deciding experiment on the question of whether light is a particle or a wave. It is thus an example of an experimentum crucis.
At that time, many favored Isaac Newton's corpuscular theory of light, among them the theoretician Siméon Denis Poisson.[10] In 1818 the French Academy of Sciences launched a competition to explain the properties of light, where Poisson was one of the members of the judging committee. The civil engineer Augustin-Jean Fresnel entered this competition by submitting a new wave theory of light.[11]
Poisson studied Fresnel's theory in detail and, being a supporter of the particle theory of light, looked for a way to prove it wrong. Poisson thought that he had found a flaw when he argued that a consequence of Fresnel's theory was that there would exist an on-axis bright spot in the shadow of a circular obstacle, where there should be complete darkness according to the particle theory of light. This prediction was seen as an absurd consequence of the wave theory, and the failure of that prediction should be a strong argument to reject Fresnel's theory.
However, the head of the committee, Dominique-François-Jean Arago, decided to actually perform the experiment. He molded a 2 mm metallic disk to a glass plate with wax.[12] He succeeded in observing the predicted spot, which convinced most scientists of the wave nature of light and gave Fresnel the win.[13]
Arago later noted[citation needed] that the phenomenon (later known as "Poisson's spot" or the "spot of Arago") had already been observed by Delisle[14] and Maraldi[15] a century earlier.
Although Arago's experimental result was overwhelming evidence in favor of the wave theory, a century later, in conjunction with the birth of quantum mechanics (and first suggested in one of Albert Einstein's Annus Mirabilis papers), it became understood that light (as well as all forms of matter and energy) must be described as both a particle and a wave (wave–particle duality). However the particle associated with electromagnetic waves, the photon, has nothing in common with the particles imagined in the corpuscular theory that had been dominant before the rise of the wave theory and Arago's powerful demonstration. Before the advent of quantum theory in the late 1920s, only the wave nature of light could explain phenomena such as diffraction and interference. Today it is known that a diffraction pattern appears through the mosaic-like buildup of bright spots caused by single photons, as predicted by Dirac's quantum theory. With increasing light intensity the bright dots in the mosaic diffraction pattern just assemble faster. In contrast, the wave theory predicts the formation of an extended continuous pattern whose overall brightness increases with light intensity.
Theory
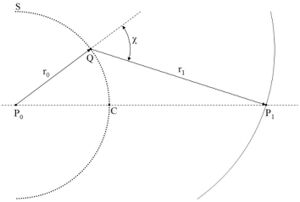
At the heart of Fresnel's wave theory is the Huygens–Fresnel principle, which states that every unobstructed point of a wavefront becomes the source of a secondary spherical wavelet and that the amplitude of the optical field E at a point on the screen is given by the superposition of all those secondary wavelets taking into account their relative phases.[16] This means that the field at a point P1 on the screen is given by a surface integral: [math]\displaystyle{ U(P_1) = \frac{A e^{\mathbf{i} k r_0}}{r_0} \int_S \frac{e^{\mathbf{i} k r_1}}{r_1} K(\chi) \, dS, }[/math] where the inclination factor [math]\displaystyle{ K(\chi) }[/math] which ensures that the secondary wavelets do not propagate backwards is given by [math]\displaystyle{ K(\chi) = \frac{\mathbf{i}}{2 \lambda} (1 + \cos(\chi)) }[/math] and
- A is the amplitude of the source wave
- [math]\displaystyle{ k = \frac{2\pi}{\lambda} }[/math] is the wavenumber
- S is the unobstructed surface.
The first term outside of the integral represents the oscillations from the source wave at a distance r0. Similarly, the term inside the integral represents the oscillations from the secondary wavelets at distances r1.
In order to derive the intensity behind the circular obstacle using this integral one assumes that the experimental parameters fulfill the requirements of the near-field diffraction regime (the size of the circular obstacle is large compared to the wavelength and small compared to the distances g = P0C and b = CP1). Going to polar coordinates[dubious ] then yields the integral for a circular object of radius a (see for example Born and Wolf[17]): [math]\displaystyle{ U(P_1) = - \frac{\mathbf{i}}{\lambda} \frac{A e^{\mathbf{i} k (g + b)}}{g b} 2\pi \int_a^\infty e^{\mathbf{i} k \frac{1}{2} \left(\frac{1}{g} + \frac{1}{b}\right) r^2} r \, dr. }[/math]
This integral can be solved numerically[dubious ] (see below). If g is large and b is small so that the angle [math]\displaystyle{ \chi }[/math] is not negligible[dubious ] one can write the integral for the on-axis case (P1 is at the center of the shadow) as (see [18]): [math]\displaystyle{ U(P_1) = \frac{A e^{\mathbf{i} k g}}{g} \frac{b}{\sqrt{b^2 + a^2}} e^{\mathbf{i} k \sqrt{b^2 + a^2}}. }[/math]
The source intensity, which is the square of the field amplitude, is [math]\displaystyle{ I_0 = \left|\frac{1}{g} A e^{\mathbf{i} k g}\right|^2 }[/math] and the intensity at the screen [math]\displaystyle{ I = \left| U(P_1) \right|^2 }[/math]. The on-axis intensity as a function of the distance b is hence given by: [math]\displaystyle{ I = \frac{b^2}{b^2 + a^2} I_0. }[/math]
This shows that the on-axis intensity at distances b much greater than the diameter of the circular obstacle is the same as the source intensity, as if the circular object was not present at all. However at larger distances b, it turns out that the size of the bright spot (as can be seen in the simulations below where b/a is increased in successive images) is larger therefore making the spot easier to discern.
Calculation of diffraction images
To calculate the full diffraction image that is visible on the screen one has to consider the surface integral of the previous section. One cannot exploit circular symmetry anymore, since the line between the source and an arbitrary point on the screen does not pass through the center of the circular object. With the aperture function [math]\displaystyle{ g(r,\theta) }[/math] which is 1 for transparent parts of the object plane and 0 otherwise (i.e. It is 0 if the direct line between source and the point on the screen passes through the blocking circular object.) the integral that needs to be solved is given by: [math]\displaystyle{ U(P_1) \propto \int_0^{2\pi} \int_0^\infty g(r,\theta) e^{\frac{\mathbf{i} \pi \rho^2}{\lambda} \left( \frac{1}{g} + \frac{1}{b} \right)} \rho \, d\rho \, d\theta. }[/math]
Numerical calculation of the integral using the trapezoidal rule or Simpson's rule is not efficient and becomes numerically unstable especially for configurations with large Fresnel number. However, it is possible to solve the radial part of the integral so that only the integration over the azimuth angle remains to be done numerically.[19] For a particular angle one must solve the line integral for the ray with origin at the intersection point of the line P0P1 with the circular object plane. The contribution for a particular ray with azimuth angle [math]\displaystyle{ \theta_1 }[/math] and passing a transparent part of the object plane from [math]\displaystyle{ r = s }[/math] to [math]\displaystyle{ r = t }[/math] is: [math]\displaystyle{ R(\theta_1) \propto e^{\frac{\pi}{2} \mathbf{i} s^2} - e^{\frac{\pi}{2} \mathbf{i} t^2}. }[/math]
So for each angle one has to compute the intersection point(s) of the ray with the circular object and then sum the contributions [math]\displaystyle{ I(\theta_1) }[/math] for a certain number of angles between 0 and [math]\displaystyle{ 2\pi }[/math]. Results of such a calculation are shown in the following images.
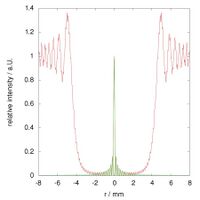
The images are simulations of the Arago spot in the shadow of discs of diameter 4 mm, 2 mm, and 1 mm, imaged 1 m behind each disc. The disks are illuminated by light of wavelength of 633 nm, diverging from a point 1 m in front of each disc. Each image is 16 mm wide.
Experimental aspects
Intensity and size
For an ideal point source, the intensity of the Arago spot equals that of the undisturbed wave front. Only the width of the Arago spot intensity peak depends on the distances between source, circular object and screen, as well as the source's wavelength and the diameter of the circular object. This means that one can compensate for a reduction in the source's wavelength by increasing the distance l between circular object and screen or reducing the circular object's diameter.
The lateral intensity distribution on the screen has in fact the shape of a squared zeroth Bessel function of the first kind when close to the optical axis and using a plane wave source (point source at infinity):[20] [math]\displaystyle{ U(P_1, r) \propto J_0^2 \left(\frac{\pi r d}{\lambda b}\right) }[/math] where
- r is the distance of the point P1 on the screen from the optical axis
- d is the diameter of circular object
- λ is the wavelength
- b is the distance between circular object and screen.
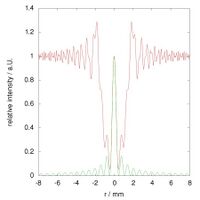
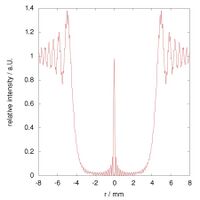
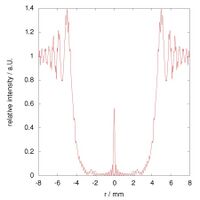
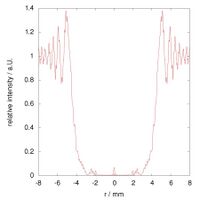
The following images show the radial intensity distribution of the simulated Arago spot images above:
The red lines in these three graphs correspond to the simulated images above, and the green lines were computed by applying the corresponding parameters to the squared Bessel function given above.
Finite source size and spatial coherence
The main reason why the Arago spot is hard to observe in circular shadows from conventional light sources is that such light sources are bad approximations of point sources. If the wave source has a finite size S then the Arago spot will have an extent that is given by Sb/g, as if the circular object acted like a lens.[16] At the same time the intensity of the Arago spot is reduced with respect to the intensity of the undisturbed wave front. Defining the relative intensity [math]\displaystyle{ I_\text{rel} }[/math]as the intensity divided by the intensity of the undisturbed wavefront, the relative intensity for an extended circular source of diameter w can be expressed exactly using the following equation:[21] [math]\displaystyle{ I_\text{rel}(w) = J_0^2\left(\frac{w R \pi}{g \lambda}\right) + J_1^2\left(\frac{w R \pi}{g \lambda}\right) }[/math] where [math]\displaystyle{ J_0 }[/math]and [math]\displaystyle{ J_1 }[/math]are the Bessel functions of the first kind. [math]\displaystyle{ R }[/math] is the radius of the disc casting the shadow, [math]\displaystyle{ \lambda }[/math] the wavelength and [math]\displaystyle{ g }[/math] the distance between source and disc. For large sources the following asymptotic approximation applies:[21] [math]\displaystyle{ I_\text{rel}(w) \approx \frac{2 g \lambda }{\pi^2 w R} }[/math]
Deviation from circularity
If the cross-section of the circular object deviates slightly from its circular shape (but it still has a sharp edge on a smaller scale) the shape of the point-source Arago spot changes. In particular, if the object has an ellipsoidal cross-section the Arago spot has the shape of an evolute.[22] Note that this is only the case if the source is close to an ideal point source. From an extended source the Arago spot is only affected marginally, since one can interpret the Arago spot as a point-spread function. Therefore, the image of the extended source only becomes washed out due to the convolution with the point-spread function, but it does not decrease in overall intensity.
The circular object's surface roughness
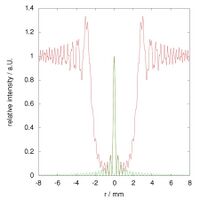
The Arago spot is very sensitive to small-scale deviations from the ideal circular cross-section. This means that a small amount of surface roughness of the circular object can completely cancel out the bright spot. This is shown in the following three diagrams which are simulations of the Arago spot from a 4 mm diameter disc (g = b = 1 m):
The simulation includes a regular sinusoidal corrugation of the circular shape of amplitude 10 μm, 50 μm and 100 μm, respectively. Note, that the 100 μm edge corrugation almost completely removes the central bright spot.
This effect can be best understood using the Fresnel zone concept. The field transmitted by a radial segment that stems from a point on the obstacle edge provides a contribution whose phase is tight to the position of the edge point relative to Fresnel zones. If the variance in the radius of the obstacle are much smaller than the width of Fresnel zone near the edge, the contributions form radial segments are approximately in phase and interfere constructively. However, if random edge corrugation have amplitude comparable to or greater than the width of that adjacent Fresnel zone, the contributions from radial segments are no longer in phase and cancel each other reducing the Arago spot intensity.
The adjacent Fresnel zone is approximately given by:[23] [math]\displaystyle{ \Delta r \approx \sqrt{r^2 + \lambda \frac{g b}{g + b}} - r. }[/math]
The edge corrugation should not be much more than 10% of this width to see a close to ideal Arago spot. In the above simulations with the 4 mm diameter disc the adjacent Fresnel zone has a width of about 77 μm.
Arago spot with matter waves
In 2009, the Arago spot experiment was demonstrated with a supersonic expansion beam of deuterium molecules (an example of neutral matter waves).[23] Material particles behaving like waves is known from quantum mechanics. The wave-nature of particles actually dates back to de Broglie's hypothesis[24] as well as Davisson and Germer's experiments.[25] An Arago spot of electrons, which also constitute matter waves, can be observed in transmission electron microscopes when examining circular structures of a certain size.
The observation of an Arago spot with large molecules, thus proving their wave-nature, is a topic of current research.[23]
Other applications
Beside the demonstration of wave-behavior, the Arago spot also has a few other applications. One of the ideas is to use the Arago spot as a straight line reference in alignment systems.[26] Another is to probe aberrations in laser beams by using the spot's sensitivity to beam aberrations.[20] Finally, the aragoscope has been proposed as a method for dramatically improving the diffraction-limited resolution of space-based telescopes.[27][28]
See also
References
- ↑ Law, Jonathan; Rennie, Richard (2015), "Poisson's Spot", A Dictionary of Physics, Oxford University Press, p. 444, SBN-10: 0198714742, ISBN 978-0198714743
- ↑ Hecht, Eugene; Zajac, Alfred (1974), "10.3, "Diffraction,"", Optics (1st ed.), Addison Wesley, p. 374, ISBN 0-201-02835-2
- ↑ "Although this phenomenon is often called Poisson's spot, Poisson probably was not happy to have seen it because it supported the wave model of light. The spot is sometimes called Fresnel's spot because it is a direct consequence of his work, and Arago's spot because Arago devised the experiment that confirmed its existence." Katz, Debora M., Physics for Scientists and Engineers: Foundations and Connections, Advance Edition, Volume 2, Cengage Learning, 2015. ISBN:1305537203
- ↑ Pedrotti, Frank L.; Pedrotti, Leno S.; Pedrotti, Leno M. (2007), Introduction to Optics (3rd ed.), Upper Saddle River, New Jersey: Pearson Education, p. 315, ISBN 978-0-13-149933-1
- ↑ Walker, Jearl (2008), Fundamentals of Physics (8th ed.), John Wiley & Sons, p. 992, ISBN 978-0-470-04472-8
- ↑ Ohanian, Hans (1989), Physics (2nd ed.), W.W. Norton, p. 984, ISBN 0-393-95786-1, https://archive.org/details/physicsvolume1se00han_xv7/page/984
- ↑ Hecht, Eugene (2002), Optics (4th ed.), Pearson Education, p. 494, ISBN 0-321-18878-0
- ↑ "Poisson's Spot". http://www.princeton.edu/~rvdb/images/Questar/PoissonSpot.html.
- ↑ Young, Thomas (1807), A Course of Lectures on Natural Philosophy and the Mechanical Arts, London: Joseph Johnson, ISBN 9780384704060, https://books.google.com/books?id=YPRZAAAAYAAJ
- ↑ Newton, Isaac (1704), Opticks: Or, A Treatise of the Reflections, Refractions, Inflections and Colours of Light, London: Royal Society, https://books.google.com/books?id=TwhbAAAAQAAJ
- ↑ OEuvres Completes 1, Paris: Imprimerie impériale, 1868, https://books.google.com/books?id=3QgAAAAAMAAJ
- ↑ Fresnel 1868, p. 369
- ↑ Arago (1819). "Rapport fait par M. Arago à l'Académie des Sciences, au nom de la Commission qui avait été chargée d'examiner les Mémoires envoyés au concours pour le prix de la diffraction." (in fr). Annales de Chimie et de Physique. 2nd series 11: 5–30. https://babel.hathitrust.org/cgi/pt?id=iau.31858046217711;view=1up;seq=11. From p. 16: "L'un de vos commissaires, M. Poisson, avait déduit des intégrales rapportées par l'auteur, le résultat singulier que le centre de l'ombre d'un écran circulaire opaque devait, lorsque les rayons y pénétraient sous des incidences peu obliques, être aussi éclairé que si l'écran n'existait pas. Cette conséquence a été soumise à l'épreuve d'une expérience directe, et l'observation a parfaitement confirmé le calcul (e)." (One of your commissioners, Mr. Poisson, had deduced from the integrals [that had been] reported by the author [i.e., Mr. Fresnel], the strange result that the center of the shadow of an opaque circular screen should — when the [light] rays penetrate it [i.e., the shadow] at slightly oblique incidences — also be illuminated as if the screen didn't exist. This result has been submitted to the test of a direct experiment, and observation has perfectly confirmed the calculation (e).)
- ↑ Delisle, J.-N. (1715). "Sur l'expérience que j'ai rapportée à l'Academie d'un anneau lumineux semblable à celui que l'on apperçoit autour de la lune dans les eclipses totales du soleil" (in fr). Histoire de l'Académie Royale des Sciences ... Avec les Mémoires de Mathématique & de Physique: 166–169. http://gallica.bnf.fr/ark:/12148/bpt6k3592w/f300.image.langFR. Delisle mentions that when a small ball was illuminated by sunlight, the ball's shadow contained alternating bright and dark rings concentric with the center of the ball's shadow.
- ↑ Maraldi, G.F. (1723). "Diverses expèriences d'optique" (in fr). Histoire de l'Académie Royale des Sciences ... Avec les Mémoires de Mathématique & de Physique: 111–143. https://www.biodiversitylibrary.org/item/88438#page/255/mode/1up. From p. 140: "La lumiere plus grande au milieu des boules plus petites, fait voir qu'elle circule en plus grande abondance & plus facilement autour des petites boules qu'autour des grandes." (More light in the middle of the smaller balls shows that it [i.e., light] spreads in greater abundance and more easily around small balls than around big [ones].) Fig. 8 on Plate 6 (following p. 142) shows light at the center of a ball's shadow.
- ↑ 16.0 16.1 Sommerfeld, Arnold (1978) (in de), Vorlesungen über Theoretische Physik: Optik, 4 (3rd ed.), Verlag Harri Deutsch, ISBN 3-87144-377-8, https://archive.org/details/vorlesungenubert0004somm
- ↑ Born, Max; Wolf, Emil (1999), Principles of optics (7th, expanded ed.), Cambridge University Press, ISBN 0-521-64222-1
- ↑ Sommerfeld 1978, p. 186
- ↑ Dauger, D.E. (November 1996), "Simulation and Study of Fresnel Diffraction for Arbitrary Two-Dimensional Apertures", Computers in Physics (AIOP) 10 (6): 591–604, doi:10.1063/1.168584, Bibcode: 1996ComPh..10..591D
- ↑ 20.0 20.1 Harvey, James E.; Forgham, James L. (1984), "The spot of Arago: New relevance for an old phenomenon", American Journal of Physics (AAPT) 52 (3): 243–247, doi:10.1119/1.13681, Bibcode: 1984AmJPh..52..243H, http://link.aip.org/link/?AJP/52/243/1
- ↑ 21.0 21.1 Reisinger, T; Leufke, P M; Gleiter, H; Hahn, H (2017-03-14). "On the relative intensity of Poisson's spot". New Journal of Physics 19 (3): 033022. doi:10.1088/1367-2630/aa5e7f. ISSN 1367-2630. Bibcode: 2017NJPh...19c3022R.
- ↑ Coulson, John; Becknell, G. G. (1922), "Reciprocal Diffraction Relations between Circular and Elliptical Plates", Phys. Rev. (American Physical Society) 20 (6): 594–600, doi:10.1103/PhysRev.20.594, Bibcode: 1922PhRv...20..594C
- ↑ 23.0 23.1 23.2 Reisinger, Thomas; Patel, A. Amil; Reingruber, Herbert; Fladischer, Katrin; Ernst, Wolfgang E.; Bracco, Gianangelo; Smith, Henry I. (2009), "Poisson's spot with molecules", Phys. Rev. A (American Physical Society) 79 (5): 053823, doi:10.1103/PhysRevA.79.053823, Bibcode: 2009PhRvA..79e3823R, http://dspace.mit.edu/bitstream/1721.1/51340/1/Reisinger-2009-Poisson%27s%20spot%20with.pdf
- ↑ de Broglie, Louis (1923), "Waves and Quanta", Nature 112 (2815): 540, doi:10.1038/112540a0, Bibcode: 1923Natur.112..540D
- ↑ Davisson, C.; Germer, L. (1927), "Diffraction of Electrons by a Crystal of Nickel", Nature 119 (2998): 558, doi:10.1038/119558a0, Bibcode: 1927Natur.119..558D
- ↑ Feier et al.
- ↑ "The Aragoscope: Ultra-High Resolution Optics at Low Cost". https://www.nasa.gov/content/the-aragoscope-ultra-high-resolution-optics-at-low-cost/#.U5givlKSz8s.
- ↑ "New space telescope concept could image objects at far higher resolution than Hubble". 23 January 2015. http://www.colorado.edu/today/2015/01/23/new-space-telescope-concept-could-image-objects-far-higher-resolution-hubble.
 |