Physics:Tait equation
In fluid mechanics, the Tait equation is an equation of state, used to relate liquid density to hydrostatic pressure. The equation was originally published by Peter Guthrie Tait in 1888 in the form[1]
- [math]\displaystyle{ \frac{V_0 - V}{P V_0} = \frac{A}{\Pi + P} }[/math]
where [math]\displaystyle{ P }[/math] is the hydrostatic pressure in addition to the atmospheric one, [math]\displaystyle{ V_0 }[/math] is the volume at atmospheric pressure, [math]\displaystyle{ V }[/math] is the volume under additional pressure [math]\displaystyle{ P }[/math], and [math]\displaystyle{ A, \Pi }[/math] are experimentally determined parameters. A very detailed historical study on the Tait equation with the physical interpretation of the two parameters [math]\displaystyle{ A }[/math] and [math]\displaystyle{ \Pi }[/math] is given in reference.[2]
Tait-Tammann equation of state
In 1895,[3][4] the original isothermal Tait equation was replaced by Tammann with an equation of the form
- [math]\displaystyle{ {K} = -{V_0} \left ( \frac{\partial P}{\partial V} \right )_T = {V_0}\frac{(B + P)}{C} }[/math]
where [math]\displaystyle{ K }[/math] is the isothermal mixed bulk modulus. This above equation is popularly known as the Tait equation. The integrated form is commonly written
- [math]\displaystyle{ V = V_0 - C \log \left(\frac{B+P}{B+P_0}\right) }[/math]
where
- [math]\displaystyle{ V \ }[/math] is the specific volume of the substance (in units of ml/g or m3/kg)
- [math]\displaystyle{ V_0 }[/math] is the specific volume at [math]\displaystyle{ P = P_0 }[/math]
- [math]\displaystyle{ B \ }[/math] (same units as [math]\displaystyle{ P_0 }[/math]) and [math]\displaystyle{ C \ }[/math] (same units as [math]\displaystyle{ V_0 }[/math]) are functions of temperature
Pressure formula
The expression for the pressure in terms of the specific volume is
- [math]\displaystyle{ P = (B + P_0)\exp\left(-\frac{V - V_0}{C}\right) - B \,. }[/math]
A highly detailed study on the Tait-Tammann equation of state with the physical interpretation of the two empirical parameters [math]\displaystyle{ C }[/math] and [math]\displaystyle{ B }[/math] is given in chapter 3 of reference.[5] Expressions as a function of temperature for the two empirical parameters [math]\displaystyle{ C }[/math] and [math]\displaystyle{ B }[/math] are given for water, seawater, helium-4, and helium-3 in the entire liquid phase up to the critical temperature [math]\displaystyle{ T_c }[/math]. The special case of the supercooled phase of water is discussed in Appendix D of reference.[6]
Tait-Murnaghan equation of state
Another popular isothermal equation of state that goes by the name "Tait equation"[7][8] is the Murnaghan model[9] which is sometimes expressed as
- [math]\displaystyle{ \frac{V}{V_0} = \left[1 + \frac{n}{K_0}\,(P - P_0)\right]^{-1/n} }[/math]
where [math]\displaystyle{ V }[/math] is the specific volume at pressure [math]\displaystyle{ P }[/math], [math]\displaystyle{ V_0 }[/math] is the specific volume at pressure [math]\displaystyle{ P_0 }[/math], [math]\displaystyle{ K_0 }[/math] is the bulk modulus at [math]\displaystyle{ P_0 }[/math], and [math]\displaystyle{ n }[/math] is a material parameter.
Pressure formula
This equation, in pressure form, can be written as
- [math]\displaystyle{ P = \frac{K_0}{n} \left[\left(\frac{V_0}{V}\right)^n - 1\right] + P_0 = \frac{K_0}{n} \left[\left(\frac{\rho}{\rho_0}\right)^n - 1\right] + P_0 . }[/math]
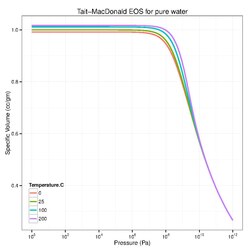
where [math]\displaystyle{ \rho, \rho_0 }[/math] are mass densities at [math]\displaystyle{ P, P_0 }[/math], respectively. For pure water, typical parameters are [math]\displaystyle{ P_0 }[/math] = 101,325 Pa, [math]\displaystyle{ \rho_0 }[/math] = 1000 kg/cu.m, [math]\displaystyle{ K_0 }[/math] = 2.15 GPa, and [math]\displaystyle{ n }[/math] = 7.15.[citation needed]
Note that this form of the Tate equation of state is identical to that of the Murnaghan equation of state.
Bulk modulus formula
The tangent bulk modulus predicted by the MacDonald–Tait model is
- [math]\displaystyle{ K = K_0\left(\frac{V_0}{V}\right)^n \,. }[/math]
Tumlirz–Tammann–Tait equation of state
A related equation of state that can be used to model liquids is the Tumlirz equation (sometimes called the Tammann equation and originally proposed by Tumlirz in 1909 and Tammann in 1911 for pure water).[4][10] This relation has the form
- [math]\displaystyle{ V(P,S,T) = V_\infty - K_1 S + \frac{\lambda}{P_0 + K_2 S + P} }[/math]
where [math]\displaystyle{ V(P,S,T) }[/math] is the specific volume, [math]\displaystyle{ P }[/math] is the pressure, [math]\displaystyle{ S }[/math] is the salinity, [math]\displaystyle{ T }[/math] is the temperature, and [math]\displaystyle{ V_\infty }[/math] is the specific volume when [math]\displaystyle{ P=\infty }[/math], and [math]\displaystyle{ K_1, K_2, P_0 }[/math] are parameters that can be fit to experimental data.
The Tumlirz–Tammann version of the Tait equation for fresh water, i.e., when [math]\displaystyle{ S = 0 }[/math], is
- [math]\displaystyle{ V = V_\infty + \frac{\lambda}{P_0 + P} \,. }[/math]
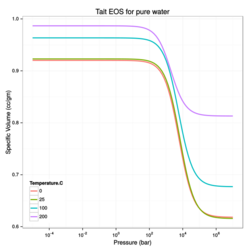
For pure water, the temperature-dependence of [math]\displaystyle{ V_\infty , \lambda, P_0 }[/math] are:[10]
- [math]\displaystyle{ \begin{align} \lambda &= 1788.316 + 21.55053\, T - 0.4695911\, T^2 + 3.096363 \times 10^{-3}\, T^3 - 0.7341182 \times 10^{-5}\, T^4 \\ P_0 &= 5918.499 + 58.05267\, T - 1.1253317\, T^2 + 6.6123869 \times 10^{-3}\, T^3 - 1.4661625 \times 10^{-5}\, T^4 \\ V_\infty &= 0.6980547 - 0.7435626 \times 10^{-3}\, T + 0.3704258 \times 10^{-4}\, T^2 - 0.6315724 \times 10^{-6}\, T^3 \\ & + 0.9829576 \times 10^{-8}\, T^4 - 0.1197269 \times 10^{-9} \,T^5 + 0.1005461 \times 10^{-11}\,T^6 \\ & - 0.5437898 \times 10^{-14} \,T^7 + 0.169946 \times 10^{-16}\, T^8 - 0.2295063 \times 10^{-19}\, T^9 \end{align} }[/math]
In the above fits, the temperature [math]\displaystyle{ T }[/math] is in degrees Celsius, [math]\displaystyle{ P_0 }[/math] is in bars, [math]\displaystyle{ V_\infty }[/math] is in cc/gm, and [math]\displaystyle{ \lambda }[/math] is in bars-cc/gm.
Pressure formula
The inverse Tumlirz–Tammann–Tait relation for the pressure as a function of specific volume is
- [math]\displaystyle{ P = \frac{\lambda}{V - V_\infty} - P_0 \,. }[/math]
Bulk modulus formula
The Tumlirz-Tammann-Tait formula for the instantaneous tangent bulk modulus of pure water is a quadratic function of [math]\displaystyle{ P }[/math] (for an alternative see [4])
- [math]\displaystyle{ K = -V\,\frac{\partial P}{\partial V} = \frac{V\,\lambda}{(V - V_\infty)^2} = (P_0 + P) + \frac{V_\infty}{\lambda}(P_0 + P)^2\,. }[/math]
Modified Tait equation of state
Following in particular the study of underwater explosions and more precisely the shock waves emitted, J.G. Kirkwood proposed in 1965[11] a more appropriate form of equation of state to describe high pressures (>1 kbar) by expressing the isentropic compressibility coefficient as
- [math]\displaystyle{ -\frac{1}{V} \left ( \frac{\partial V}{\partial P} \right )_S = \frac{1}{n(B + P)} }[/math]
where [math]\displaystyle{ S }[/math] represents here the entropy. The two empirical paramaters [math]\displaystyle{ n }[/math] and [math]\displaystyle{ B }[/math] are now function of entropy such that
- [math]\displaystyle{ n \ }[/math] is dimensionless
- [math]\displaystyle{ B \ }[/math] has the same units as [math]\displaystyle{ P }[/math]
The integration leads to the following expression for the volume [math]\displaystyle{ V(P,S) }[/math] along the isentropic [math]\displaystyle{ S }[/math]
- [math]\displaystyle{ \frac{V}{V_0} = \left(1 + \frac{P_0}{B}\right)^{1/n} \left(1 + \frac{P}{B}\right)^{-1/n} }[/math]
where [math]\displaystyle{ V_0 = V(P_0, S) }[/math].
Pressure formula
The expression for the pressure [math]\displaystyle{ P(V,S) }[/math] in terms of the specific volume along the isentropic [math]\displaystyle{ S }[/math] is
- [math]\displaystyle{ P = (B + P_0)\,\left(\cfrac{V_0}{V}\right)^n - B \,. }[/math]
A highly detailed study on the Modified Tait equation of state with the physical interpretation of the two empirical parameters [math]\displaystyle{ n }[/math] and [math]\displaystyle{ B }[/math] is given in chapter 4 of reference.[12] Expressions as a function of entropy for the two empirical parameters [math]\displaystyle{ n }[/math] and [math]\displaystyle{ B }[/math] are given for water, helium-3 and helium-4.
See also
References
- ↑ Tait, P. G. (1888). "Report on some of the physical properties of fresh water and of sea water". Physics and Chemistry of the Voyage of H.M.S. Challenger. II, part IV.
- ↑ Aitken, Frederic; Foulc, Jean-Numa (2019). From Deep Sea to Laboratory 3:From Tait's Work on the Compressibility of Seawater to Equations-of-State for Liquids. London, UK: ISTE - WILEY. ISBN 9781786303769. http://www.iste.co.uk/book.php?id=1534.
- ↑ Tammann, G. (1895). "Über die Abhängigkeit der volumina von Lösungen vom druck". Zeitschrift für Physikalische Chemie 17: 620-636.
- ↑ 4.0 4.1 4.2 Hayward, A. T. J. (1967). Compressibility equations for liquids: a comparative study. British Journal of Applied Physics, 18(7), 965. http://mitran-lab.amath.unc.edu:8081/subversion/Lithotripsy/MultiphysicsFocusing/biblio/TaitEquationOfState/Hayward_CompressEqnsLiquidsComparative1967.pdf
- ↑ Aitken, Frederic; Foulc, Jean-Numa (2019). From Deep Sea to Laboratory 3:From Tait's Work on the Compressibility of Seawater to Equations-of-State for Liquids. London, UK: ISTE - WILEY. ISBN 9781786303769. http://www.iste.co.uk/book.php?id=1534.
- ↑ Aitken, F.; Volino, F. (November 2021). "A new single equation of state to describe the dynamic viscosity and self-diffusion coefficient for all fluid phases of water from 200 to 1800 K based on a new original microscopic model". Physics of Fluids 33 (11): 117112. doi:10.1063/5.0069488. Bibcode: 2021PhFl...33k7112A.
- ↑ Thompson, P. A., & Beavers, G. S. (1972). Compressible-fluid dynamics. Journal of Applied Mechanics, 39, 366.
- ↑ Kedrinskiy, V. K. (2006). Hydrodynamics of Explosion: experiments and models. Springer Science & Business Media.
- ↑ Macdonald, J. R. (1966). Some simple isothermal equations of state. Reviews of Modern Physics, 38(4), 669.
- ↑ 10.0 10.1 Fisher, F. H., and O. E. Dial Jr. Equation of state of pure water and sea water. No. MPL-U-99/67. SCRIPPS INSTITUTION OF OCEANOGRAPHY LA JOLLA CA MARINE PHYSICAL LAB, 1975. http://www.dtic.mil/dtic/tr/fulltext/u2/a017775.pdf
- ↑ Cole, R. H. (1965). Underwater Explosions. New York: Dover Publications.
- ↑ Aitken, Frederic; Foulc, Jean-Numa (2019). From Deep Sea to Laboratory 3:From Tait's Work on the Compressibility of Seawater to Equations-of-State for Liquids. London, UK: ISTE - WILEY. ISBN 9781786303769. http://www.iste.co.uk/book.php?id=1534.
 |