Physics:Bimodal atomic force microscopy

From HandWiki
Revision as of 04:44, 5 February 2024 by QCDvac (talk | contribs) (change)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Excitation and detection scheme in bimodal AFM. The cantilever is excited at its first two eigenmodes with frequencies [math]\displaystyle{ f_1 }[/math] and [math]\displaystyle{ f_2 }[/math]. Upon interaction with the sample, the components of the tip's response are processed. The topography is obtained by keeping [math]\displaystyle{ A_1 }[/math]= constant. In a bimodal AM-FM configuration, two feedback loops act on the 2nd mode. One keeps [math]\displaystyle{ A_2 }[/math] fixed while a phase-lock loop keeps [math]\displaystyle{ \phi_2=90^o }[/math].

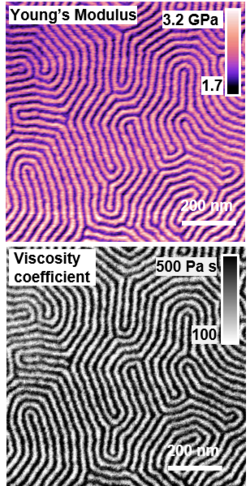
Bimodal Atomic Force Microscopy (bimodal AFM) is an advanced atomic force microscopy technique characterized by generating high-spatial resolution maps of material properties. Topography, deformation, elastic modulus, viscosity coefficient or magnetic field maps might be generated. Bimodal AFM is based on the simultaneous excitation and detection of two eigenmodes (resonances) of a force microscope microcantilever.

History

Numerical and theoretical considerations[1][2] prompted the development of bimodal AFM. The method was initially thought to enhance topographic contrast in air environments.[3][4] Three subsequent advances such as the capability to detect non-topography properties such electrostatic[5] and magnetic[6] interactions; imaging in liquid[7] and ultra-high vacuum[8] and its genuine quantitative features[9][10] set the stage for further developments and applications.

Principles of Bimodal AFM

Nanomechanical maps of a polymer blend generated by bimodal AFM. Young's modulus (top) and viscosity coefficient (bottom) maps of a PS-b-PMMA block co-polymer. The stiffer domains (PMMA) show a lower viscosity coefficient and a faster response time.
Angstrom-scale resolution. Topography (top) and elastic modulus (middle) maps of metal-organic-framework (MOF). The MOF structure on the basal plane is being overlaid. Angstrom-scale variations of the elastic modulus are associated with the chemical structure of the MOF. Distribution of the elastic modulus values. Data obtained from the middle map (bottom). The curve can be decomposed in four individual Gaussian curves, centered respectively, at 25.7, 27.5, 29.3 and 32.3 GPa.

The interaction of the tip with the sample modifies the amplitudes, phase shifts and frequency resonances of the excited modes. Those changes are detected and processed by the feedback of the instrument. Several features make bimodal AFM a very powerful surface characterization method at the nanoscale. (i) Resolution. Atomic, molecular or nanoscale spatial resolution was demonstrated. (ii) Simultaneity. Maps of different properties are generated at the same time. (iii) Efficiency. A maximum number of four data points per pixel are needed to generate material property maps. (iv) Speed. Analytical solutions link observables with material properties.

Configurations

In AFM, feedback loops control the operation of the microscope by keeping a fixed value a parameter of the tip's oscillation.[11] If the main feedback loop operates with the amplitude, the AFM mode is called amplitude modulation (AM). If it operates with the frequency shift, the AFM mode is called frequency modulation (FM). Bimodal AFM might be operated with several feedback loops. This gives rise to a variety of bimodal configurations.[12] The configurations are termed AM-open loop, AM-FM, FM-FM.[13] For example, bimodal AM-FM means that the first mode is operated with an amplitude modulation loop while the 2nd mode is operated with a frequency modulation loop. The configurations might not be equivalent in terms of sensitivity, signal-to-noise ratio or complexity.

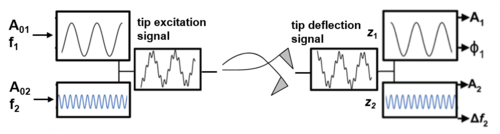
Let's consider the AM-FM configuration. The first mode is excited to reach free amplitude (no interaction) and the changes of its amplitude and phase shift are tracked by a lock-in amplifier. The main feedback loop keeps constant the amplitude, at a certain set-point [math]\displaystyle{ A_1 }[/math] by modifying the tip vertical position (AM). In a nanomechanical mapping experiment, [math]\displaystyle{ \phi_1 }[/math] must be kept below 90°, i.e., the AFM is operated in the repulsive regime. At the same time, an FM loop acts on the second eigenmode. A phase-lock-loop regulates the excitation frequency [math]\displaystyle{ f_2 }[/math] by keeping the phase shift of the second mode at 90°. An additional feedback loop might be used to maintain the amplitude [math]\displaystyle{ A_2 }[/math] constant.

Theory

The theory of bimodal AFM operation encompasses several aspects. Among them, the approximations to express the Euler-Bernoulli equation of a continuous cantilever beam in terms of the equations of the excited modes,[2][8][10][14] the type of interaction forces acting on the tip,[15][16][17] the theory of demodulation methods[18] or the introduction of finite-size effects.[19]

In a nutshell, the tip displacement in AFM is approximated by a point-mass model,[13]

[math]\displaystyle{ \frac{k_i}{4\pi^2 f_i^2} \ddot{z_i} + \frac{k_i}{2\pi f_{0 i} Q} \dot{z_i} + k_i z_i = F_i \cos(2 \pi f_i t) + F_{ts} (t) \, }[/math]

where [math]\displaystyle{ f_i }[/math], [math]\displaystyle{ f_0i }[/math], [math]\displaystyle{ Q_i }[/math], [math]\displaystyle{ k_i }[/math], [math]\displaystyle{ F_i }[/math], and [math]\displaystyle{ F_{ts} }[/math] are, respectively, the driving frequency, the free resonant frequency, the quality factor, the stiffness, the driving force of the i-th mode, and the tip–sample interaction force. In bimodal AFM, the vertical motion of the tip (deflection) has two components, one for each mode,

[math]\displaystyle{ z(t) = z_0 +z_1(t)+z_2(t) \approx A_1 cos \left(2\pi f_1 t - \phi_1 \right) + A_2 cos \left(2\pi f_2 t - \frac{\pi}{2} \right) \, }[/math]

with [math]\displaystyle{ z_0 }[/math], [math]\displaystyle{ z_1 }[/math], [math]\displaystyle{ z_2 }[/math], as the static, the first, and the second mode deflections; [math]\displaystyle{ A_i }[/math], [math]\displaystyle{ f_i }[/math] and [math]\displaystyle{ \phi_i }[/math] are, respectively, the amplitude, frequency and phase shift of mode i.

The theory that transforms bimodal AFM observables into material properties is based on applying the virial [math]\displaystyle{ V_i }[/math] and energy dissipation [math]\displaystyle{ E_{diss} }[/math] theorems to the equations of motion of the excited modes. The following equations were derived[20]

[math]\displaystyle{ V_1= \frac{1}{T}\int_0^T F_{ts} (t) z_1(t) dt = - \frac{k_1 A_1 A_{01}}{2 Q_1} \cos{\phi_1} \, }[/math]

[math]\displaystyle{ V_2= \frac{1}{T}\int_0^T F_{ts} (t) z_2(t) dt \approx - \frac{k_2 A_2^2 \Delta f_2}{f_{02}} \, }[/math]

[math]\displaystyle{ E_{diss1}= \int_0^T F_{ts} (t) \dot{z}_1(t) dt = - \frac{\pi k_1 A_1 }{Q_1} (A_1 - A_{01}\sin(\phi_1)) \, }[/math]

where [math]\displaystyle{ T=T_1 T_2 }[/math] is a time where the oscillation of both modes are periodic; [math]\displaystyle{ Q_i }[/math] the quality factor of mode i. Bimodal AFM operation might be involve any pair of eigenmodes. However, experiments are commonly performed by exciting the first two eigenmodes.

The theory of bimodal AFM provides analytical expressions to link material properties with microscope observables. For example, for a paraboloid probe (radius [math]\displaystyle{ R }[/math]) and a tip-sample force given by the linear viscoelastic Kelvin-Voigt model, the effective elastic modulus [math]\displaystyle{ E_{eff} }[/math] of the sample, viscous coefficient of compressibility [math]\displaystyle{ \eta_{com} }[/math], loss tangent [math]\displaystyle{ \tan \rho }[/math] or retardation time [math]\displaystyle{ \tau }[/math] are expressed by[21]

[math]\displaystyle{ E_{eff} = 4 \sqrt{2} \frac{Q_1}{\sqrt{R}} \frac{k_2^2}{k_1} \frac{\Delta f_2^2}{f_{02}^2} \frac{A_1^{3/2}}{A_{01}^2-A_1^2} \, }[/math]

[math]\displaystyle{ \eta_{com} = \frac{E_{eff}}{\omega_1} \left[ \frac{A_{01}\sin{\phi_1}-A_1}{A_{01}\cos{\phi_1}} \right] \, }[/math]

[math]\displaystyle{ \tan \rho = 2 \pi \omega_1 \frac{\eta_{com}}{E_{eff}} = 2 \pi \omega_1 \tau \, }[/math]

For an elastic material, the second term of equation to calculate [math]\displaystyle{ \eta }[/math] disappears because [math]\displaystyle{ A_1=A_{01} \sin{\phi_1} }[/math] which gives [math]\displaystyle{ \eta = 0 }[/math]. The elastic modulus is obtained from the equation above. Other analytical expressions were proposed for the determination of the Hamaker constant[15] and the magnetic parameters of a ferromagnetic sample.[16]

Applications

Bimodal AFM is applied to characterize a large variety of surfaces and interfaces. Some applications exploit the sensitivity of bimodal observables to enhance spatial resolution. However, the full capabilities of bimodal AFM are shown in the generation of quantitative maps of material properties. The section is divided in terms of the achieved spatial resolution, atomic-scale or nanoscale.

Atomic and molecular-scale resolution

Atomic-scale imaging of graphene,[22] semiconductor surfaces[23] and adsorbed organic molecules[24] were obtained in ultra high-vacuum. Angstrom-resolution images of hydration layers formed on proteins and Young's modulus map of a metal-organic frame work, purple membrane and a lipid bilayer were reported in aqueous solutions.[20][25][26]

Material property applications

Bimodal AFM is widely used to provide high-spatial resolution maps of material properties, in particular, mechanical properties. Elastic and/or viscoelastic property maps of polymers,[27][28][29][30][31] DNA,[32] proteins, protein fibers,[33] lipids[34][19] or 2D materials[35][36] were generated. Non-mechanical properties and interactions including crystal magnetic garnets, electrostatic strain, superparamagnetic particles and high-density disks were also mapped.[37][38] Quantitative property mapping requires the calibration of the force constants of the excited modes.[39]

References

  1. ↑ Rodrı́guez, Tomás R.; Garcı́a, Ricardo (2004). "Compositional mapping of surfaces in atomic force microscopy by excitation of the second normal mode of the microcantilever". Applied Physics Letters 84 (3): 449–451. doi:10.1063/1.1642273. ISSN 0003-6951. Bibcode: 2004ApPhL..84..449R. http://aip.scitation.org/doi/10.1063/1.1642273. 
  2. ↑ 2.0 2.1 Lozano, Jose R.; Garcia, Ricardo (2008). "Theory of Multifrequency Atomic Force Microscopy". Physical Review Letters 100 (7): 076102. doi:10.1103/PhysRevLett.100.076102. ISSN 0031-9007. PMID 18352572. Bibcode: 2008PhRvL.100g6102L. https://link.aps.org/doi/10.1103/PhysRevLett.100.076102. 
  3. ↑ Proksch, Roger (2006). "Multifrequency, repulsive-mode amplitude-modulated atomic force microscopy". Applied Physics Letters 89 (11): 113121. doi:10.1063/1.2345593. ISSN 0003-6951. Bibcode: 2006ApPhL..89k3121P. http://aip.scitation.org/doi/10.1063/1.2345593. 
  4. ↑ Martinez, N. F.; Patil, S.; Lozano, J. R.; Garcia, R. (2006). "Enhanced compositional sensitivity in atomic force microscopy by the excitation of the first two flexural modes". Applied Physics Letters 89 (15): 153115. doi:10.1063/1.2360894. ISSN 0003-6951. Bibcode: 2006ApPhL..89o3115M. http://aip.scitation.org/doi/10.1063/1.2360894. 
  5. ↑ Stark, Robert W; Naujoks, Nicola; Stemmer, Andreas (2007). "Multifrequency electrostatic force microscopy in the repulsive regime". Nanotechnology 18 (6): 065502. doi:10.1088/0957-4484/18/6/065502. ISSN 0957-4484. Bibcode: 2007Nanot..18f5502S. https://iopscience.iop.org/article/10.1088/0957-4484/18/6/065502. 
  6. ↑ Li, Jason W.; Cleveland, Jason P.; Proksch, Roger (2009). "Bimodal magnetic force microscopy: Separation of short and long range forces". Applied Physics Letters 94 (16): 163118. doi:10.1063/1.3126521. ISSN 0003-6951. Bibcode: 2009ApPhL..94p3118L. http://aip.scitation.org/doi/10.1063/1.3126521. 
  7. ↑ Martínez, N F; Lozano, J R; Herruzo, E T; Garcia, F; Richter, C; Sulzbach, T; Garcia, R (2008). "Bimodal atomic force microscopy imaging of isolated antibodies in air and liquids". Nanotechnology 19 (38): 384011. doi:10.1088/0957-4484/19/38/384011. ISSN 0957-4484. PMID 21832570. Bibcode: 2008Nanot..19L4011M. https://iopscience.iop.org/article/10.1088/0957-4484/19/38/384011. 
  8. ↑ 8.0 8.1 Kawai, Shigeki; Glatzel, Thilo; Koch, Sascha; Such, Bartosz; Baratoff, Alexis; Meyer, Ernst (2009). "Systematic Achievement of Improved Atomic-Scale Contrast via Bimodal Dynamic Force Microscopy". Physical Review Letters 103 (22): 220801. doi:10.1103/PhysRevLett.103.220801. ISSN 0031-9007. PMID 20366084. Bibcode: 2009PhRvL.103v0801K. https://link.aps.org/doi/10.1103/PhysRevLett.103.220801. 
  9. ↑ Martinez-Martin, D.; Herruzo, E. T.; Dietz, C.; Gomez-Herrero, J.; Garcia, R. (2011). "Noninvasive Protein Structural Flexibility Mapping by Bimodal Dynamic Force Microscopy". Physical Review Letters 106 (19): 198101. doi:10.1103/PhysRevLett.106.198101. ISSN 0031-9007. PMID 21668203. Bibcode: 2011PhRvL.106s8101M. https://link.aps.org/doi/10.1103/PhysRevLett.106.198101. 
  10. ↑ 10.0 10.1 Herruzo, Elena T.; Perrino, Alma P.; Garcia, Ricardo (2014). "Fast nanomechanical spectroscopy of soft matter". Nature Communications 5 (1): 3126. doi:10.1038/ncomms4126. ISSN 2041-1723. PMID 24445593. Bibcode: 2014NatCo...5.3126H. 
  11. ↑ García, R (2002). "Dynamic atomic force microscopy methods". Surface Science Reports 47 (6–8): 197–301. doi:10.1016/S0167-5729(02)00077-8. ISSN 0167-5729. Bibcode: 2002SurSR..47..197G. https://linkinghub.elsevier.com/retrieve/pii/S0167572902000778. 
  12. ↑ Solares, Santiago D.; Chawla, Gaurav (2010). "Triple-frequency intermittent contact atomic force microscopy characterization: Simultaneous topographical, phase, and frequency shift contrast in ambient air". Journal of Applied Physics 108 (5): 054901–054901–5. doi:10.1063/1.3475644. ISSN 0021-8979. Bibcode: 2010JAP...108e4901S. http://aip.scitation.org/doi/10.1063/1.3475644. 
  13. ↑ 13.0 13.1 Garcia, Ricardo; Proksch, Roger (2013). "Nanomechanical mapping of soft matter by bimodal force microscopy". European Polymer Journal 49 (8): 1897–1906. doi:10.1016/j.eurpolymj.2013.03.037. ISSN 0014-3057. 
  14. ↑ Labuda, Aleksander; Kocuń, Marta; Meinhold, Waiman; Walters, Deron; Proksch, Roger (2016). "Generalized Hertz model for bimodal nanomechanical mapping". Beilstein Journal of Nanotechnology 7: 970–982. doi:10.3762/bjnano.7.89. ISSN 2190-4286. PMID 27547614. PMC 4979904. https://www.beilstein-journals.org/bjnano/articles/7/89. 
  15. ↑ 15.0 15.1 Lai, Chia-Yun; Santos, Sergio; Chiesa, Matteo (2016). "Systematic Multidimensional Quantification of Nanoscale Systems From Bimodal Atomic Force Microscopy Data". ACS Nano 10 (6): 6265–6272. doi:10.1021/acsnano.6b02455. ISSN 1936-0851. PMID 27172380. https://pubs.acs.org/doi/10.1021/acsnano.6b02455. 
  16. ↑ 16.0 16.1 Gisbert, Victor G.; Amo, Carlos A.; Jaafar, Miriam; Asenjo, Agustina; Garcia, Ricardo (2021). "Quantitative mapping of magnetic properties at the nanoscale with bimodal AFM". Nanoscale 13 (3): 2026–2033. doi:10.1039/D0NR08662B. ISSN 2040-3364. PMID 33449980. http://xlink.rsc.org/?DOI=D0NR08662B. 
  17. ↑ Rajabifar, Bahram; Bajaj, Anil; Reifenberger, Ronald; Proksch, Roger; Raman, Arvind (2021). "Discrimination of adhesion and viscoelasticity from nanoscale maps of polymer surfaces using bimodal atomic force microscopy". Nanoscale 13 (41): 17428–17441. doi:10.1039/D1NR03437E. ISSN 2040-3364. PMID 34647552. http://xlink.rsc.org/?DOI=D1NR03437E. 
  18. ↑ Harcombe, David M; Ruppert, Michael G; Fleming, Andrew J (2020). "A review of demodulation techniques for multifrequency atomic force microscopy". Beilstein Journal of Nanotechnology 11: 76–91. doi:10.3762/bjnano.11.8. ISSN 2190-4286. PMID 31976199. PMC 6964647. https://www.beilstein-journals.org/bjnano/articles/11/8. 
  19. ↑ 19.0 19.1 Gisbert, Victor G.; Garcia, Ricardo (2021). "Accurate Wide-Modulus-Range Nanomechanical Mapping of Ultrathin Interfaces with Bimodal Atomic Force Microscopy". ACS Nano 15 (12): 20574–20581. doi:10.1021/acsnano.1c09178. ISSN 1936-0851. PMID 34851086. https://pubs.acs.org/doi/10.1021/acsnano.1c09178. 
  20. ↑ 20.0 20.1 Amo, Carlos A.; Perrino, Alma P.; Payam, Amir F.; Garcia, Ricardo (2017). "Mapping Elastic Properties of Heterogeneous Materials in Liquid with Angstrom-Scale Resolution". ACS Nano 11 (9): 8650–8659. doi:10.1021/acsnano.7b04381. ISSN 1936-0851. PMID 28770996. 
  21. ↑ Benaglia, Simone; Amo, Carlos A.; Garcia, Ricardo (2019). "Fast, quantitative and high resolution mapping of viscoelastic properties with bimodal AFM". Nanoscale 11 (32): 15289–15297. doi:10.1039/C9NR04396A. ISSN 2040-3364. PMID 31386741. http://xlink.rsc.org/?DOI=C9NR04396A. 
  22. ↑ Kawai, Shigeki; Eren, Baran; Marot, Laurent; Meyer, Ernst (2014). "Graphene Synthesis via Thermal Polymerization of Aromatic Quinone Molecules". ACS Nano 8 (6): 5932–5938. doi:10.1021/nn501047v. ISSN 1936-0851. PMID 24873393. https://pubs.acs.org/doi/10.1021/nn501047v. 
  23. ↑ Naitoh, Yoshitaka; Turanský, Robert; Brndiar, Ján; Li, Yan Jun; Štich, Ivan; Sugawara, Yasuhiro (2017). "Subatomic-scale force vector mapping above a Ge(001) dimer using bimodal atomic force microscopy". Nature Physics 13 (7): 663–667. doi:10.1038/nphys4083. ISSN 1745-2473. Bibcode: 2017NatPh..13..663N. http://www.nature.com/articles/nphys4083. 
  24. ↑ Martin-Jimenez, Daniel; Ruppert, Michael G.; Ihle, Alexander; Ahles, Sebastian; Wegner, Hermann A.; Schirmeisen, André; Ebeling, Daniel (2022). "Chemical bond imaging using torsional and flexural higher eigenmodes of qPlus sensors". Nanoscale 14 (14): 5329–5339. doi:10.1039/D2NR01062C. ISSN 2040-3364. PMID 35348167. http://xlink.rsc.org/?DOI=D2NR01062C. 
  25. ↑ Garcia, Ricardo; Herruzo, Elena T. (2012). "The emergence of multifrequency force microscopy". Nature Nanotechnology 7 (4): 217–226. doi:10.1038/nnano.2012.38. ISSN 1748-3387. PMID 22466857. Bibcode: 2012NatNa...7..217G. http://www.nature.com/articles/nnano.2012.38. 
  26. ↑ Trewby, William; Faraudo, Jordi; Voïtchovsky, Kislon (2019). "Long-lived ionic nano-domains can modulate the stiffness of soft interfaces". Nanoscale 11 (10): 4376–4384. doi:10.1039/C8NR06339G. ISSN 2040-3364. PMID 30801089. http://xlink.rsc.org/?DOI=C8NR06339G. 
  27. ↑ Kocun, Marta; Labuda, Aleksander; Meinhold, Waiman; Revenko, Irène; Proksch, Roger (2017). "Fast, High Resolution, and Wide Modulus Range Nanomechanical Mapping with Bimodal Tapping Mode". ACS Nano 11 (10): 10097–10105. doi:10.1021/acsnano.7b04530. ISSN 1936-0851. PMID 28953363. https://pubs.acs.org/doi/10.1021/acsnano.7b04530. 
  28. ↑ Ebeling, Daniel; Eslami, Babak; Solares, Santiago De Jesus (2013). "Visualizing the Subsurface of Soft Matter: Simultaneous Topographical Imaging, Depth Modulation, and Compositional Mapping with Triple Frequency Atomic Force Microscopy". ACS Nano 7 (11): 10387–10396. doi:10.1021/nn404845q. ISSN 1936-0851. PMID 24131492. https://pubs.acs.org/doi/10.1021/nn404845q. 
  29. ↑ Nguyen, Hung K.; Ito, Makiko; Nakajima, Ken (2016). "Elastic and viscoelastic characterization of inhomogeneous polymers by bimodal atomic force microscopy". Japanese Journal of Applied Physics 55 (8S1): 08–06. doi:10.7567/JJAP.55.08NB06. ISSN 0021-4922. Bibcode: 2016JaJAP..55hNB06N. https://iopscience.iop.org/article/10.7567/JJAP.55.08NB06. 
  30. ↑ Dietz, Christian (2018). "Sensing in-plane nanomechanical surface and sub-surface properties of polymers: local shear stress as function of the indentation depth". Nanoscale 10 (1): 460–468. doi:10.1039/C7NR07147G. ISSN 2040-3364. PMID 29227502. http://xlink.rsc.org/?DOI=C7NR07147G. 
  31. ↑ Nguyen, Hung K.; Aoki, Mika; Liang, Xiaobin; Yamamoto, Satoru; Tanaka, Keiji; Nakajima, Ken (2021). "Local Mechanical Properties of Heterogeneous Nanostructures Developed in a Cured Epoxy Network: Implications for Innovative Adhesion Technology". ACS Applied Nano Materials 4 (11): 12188–12196. doi:10.1021/acsanm.1c02692. ISSN 2574-0970. https://pubs.acs.org/doi/10.1021/acsanm.1c02692. 
  32. ↑ Bose, Krishnashish; Lech, Christopher J.; Heddi, Brahim; Phan, Anh Tuân (2018). "High-resolution AFM structure of DNA G-wires in aqueous solution". Nature Communications 9 (1): 1959. doi:10.1038/s41467-018-04016-y. ISSN 2041-1723. PMID 29773796. Bibcode: 2018NatCo...9.1959B. 
  33. ↑ Gisbert, Victor G.; Benaglia, Simone; Uhlig, Manuel R.; Proksch, Roger; Garcia, Ricardo (2021). "High-Speed Nanomechanical Mapping of the Early Stages of Collagen Growth by Bimodal Force Microscopy". ACS Nano 15 (1): 1850–1857. doi:10.1021/acsnano.0c10159. ISSN 1936-0851. PMID 33412008. 
  34. ↑ Al-Rekabi, Zeinab; Contera, Sonia (2018). "Multifrequency AFM reveals lipid membrane mechanical properties and the effect of cholesterol in modulating viscoelasticity". Proceedings of the National Academy of Sciences 115 (11): 2658–2663. doi:10.1073/pnas.1719065115. ISSN 0027-8424. PMID 29483271. Bibcode: 2018PNAS..115.2658A. 
  35. ↑ Li, Yuhao; Yu, Chuanbin; Gan, Yingye; Jiang, Peng; Yu, Junxi; Ou, Yun; Zou, Dai-Feng; Huang, Cheng et al. (2018). "Mapping the elastic properties of two-dimensional MoS2 via bimodal atomic force microscopy and finite element simulation". npj Computational Materials 4 (1): 49. doi:10.1038/s41524-018-0105-8. ISSN 2057-3960. Bibcode: 2018npjCM...4...49L. 
  36. ↑ Lai, Chia-Yun; Santos, Sergio; Chiesa, Matteo (2019). "Machine learning assisted quantification of graphitic surfaces exposure to defined environments". Applied Physics Letters 114 (24): 241601. doi:10.1063/1.5095704. ISSN 0003-6951. Bibcode: 2019ApPhL.114x1601L. http://aip.scitation.org/doi/10.1063/1.5095704. 
  37. ↑ Dietz, Christian; Herruzo, Elena T; Lozano, Jose R; Garcia, Ricardo (2011). "Nanomechanical coupling enables detection and imaging of 5 nm superparamagnetic particles in liquid". Nanotechnology 22 (12): 125708. doi:10.1088/0957-4484/22/12/125708. ISSN 0957-4484. PMID 21325711. Bibcode: 2011Nanot..22l5708D. https://iopscience.iop.org/article/10.1088/0957-4484/22/12/125708. 
  38. ↑ Giridharagopal, R.; Flagg, L. Q.; Harrison, J. S.; Ziffer, M. E.; Onorato, J.; Luscombe, C. K.; Ginger, D.S. (2017). "Electrochemical strain microscopy probes morphology-induced variations in ion uptake and performance in organic electrochemical transistors". Nature Materials 16 (7): 737–742. doi:10.1038/nmat4918. ISSN 1476-1122. PMID 28628123. Bibcode: 2017NatMa..16..737G. http://www.nature.com/articles/nmat4918. 
  39. ↑ Labuda, Aleksander; Kocun, Marta; Lysy, Martin; Walsh, Tim; Meinhold, Jieh; Proksch, Tania; Meinhold, Waiman; Anderson, Caleb et al. (2016). "Calibration of higher eigenmodes of cantilevers". Review of Scientific Instruments 87 (7): 073705. doi:10.1063/1.4955122. ISSN 0034-6748. PMID 27475563. Bibcode: 2016RScI...87g3705L. http://aip.scitation.org/doi/10.1063/1.4955122. 



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Bimodal_atomic_force_microscopy&oldid=3281641"