Physics:Dirac cone
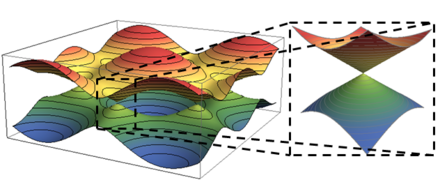
In physics, Dirac cones are features that occur in some electronic band structures that describe unusual electron transport properties of materials like graphene and topological insulators.[1][2][3] In these materials, at energies near the Fermi level, the valence band and conduction band take the shape of the upper and lower halves of a conical surface, meeting at what are called Dirac points.
Typical examples include graphene, topological insulators, bismuth antimony thin films and some other novel nanomaterials,[1][4][5] in which the electronic energy and momentum have a linear dispersion relation such that the electronic band structure near the Fermi level takes the shape of an upper conical surface for the electrons and a lower conical surface for the holes. The two conical surfaces touch each other and form a zero-band gap semimetal.
The name of Dirac cone comes from the Dirac equation that can describe relativistic particles in quantum mechanics, proposed by Paul Dirac. Isotropic Dirac cones in graphene were first predicted by P. R. Wallace in 1947[6] and experimentally observed by the Nobel Prize laureates Andre Geim and Konstantin Novoselov in 2005.[7]
Description
In quantum mechanics, Dirac cones are a kind of crossing-point which electrons avoid,[8] where the energy of the valence and conduction bands are not equal anywhere in two dimensional lattice k-space, except at the zero dimensional Dirac points. As a result of the cones, electrical conduction can be described by the movement of charge carriers which are massless fermions, a situation which is handled theoretically by the relativistic Dirac equation.[9] The massless fermions lead to various quantum Hall effects, magnetoelectric effects in topological materials, and ultra high carrier mobility.[10][11] Dirac cones were observed in 2008-2009, using angle-resolved photoemission spectroscopy (ARPES) on the potassium-graphite intercalation compound KC8.[12] and on several bismuth-based alloys.[13][14][11]
As an object with three dimensions, Dirac cones are a feature of two-dimensional materials or surface states, based on a linear dispersion relation between energy and the two components of the crystal momentum kx and ky. However, this concept can be extended to three dimensions, where Dirac semimetals are defined by a linear dispersion relation between energy and kx, ky, and kz. In k-space, this shows up as a hypercone, which have doubly degenerate bands which also meet at Dirac points.[11] Dirac semimetals contain both time reversal and spatial inversion symmetry; when one of these is broken, the Dirac points are split into two constituent Weyl points, and the material becomes a Weyl semimetal.[15][16][17][18][19][20][21][22][23][24][25] In 2014, direct observation of the Dirac semimetal band structure using ARPES was conducted on the Dirac semimetal cadmium arsenide.[26][27][28]
Analog systems
Dirac points have been realized in many physical areas such as plasmonics, phononics, or nanophotonics (microcavities,[29] photonic crystals[30]).
See also
References
- ↑ 1.0 1.1 Novoselov, K.S.; Geim, A.K. (2007). "The rise of graphene". Nature Materials 6 (3): 183–191. doi:10.1038/nmat1849. PMID 17330084. Bibcode: 2007NatMa...6..183G.
- ↑ Hasan, M.Z.; Kane, C.L. (2010). "Topological Insulators". Rev. Mod. Phys. 82 (4): 3045. doi:10.1103/revmodphys.82.3045. Bibcode: 2010RvMP...82.3045H. https://repository.upenn.edu/cgi/viewcontent.cgi?article=1043&context=physics_papers.
- ↑ "Superconductors: Dirac cones come in pairs" (in en). Tohoku University. 29 Aug 2011. http://www.wpi-aimr.tohoku.ac.jp/en/aimresearch/highlight/2011/20110829_000812.html.
- ↑ Dirac cones could exist in bismuth–antimony films. Physics World, Institute of Physics, 17 April 2012.
- ↑ Hsieh, David (2008). "A topological Dirac insulator in a quantum spin Hall phase". Nature 452 (7190): 970–974. doi:10.1038/nature06843. PMID 18432240. Bibcode: 2008Natur.452..970H. https://authors.library.caltech.edu/49766/.
- ↑ Wallace, P. R. (1947). "The Band Theory of Graphite". Physical Review 71 (9): 622–634. doi:10.1103/PhysRev.71.622. Bibcode: 1947PhRv...71..622W.
- ↑ The Nobel Prize in Physics 2010 Press Release. Nobelprize.org, 5 October 2010. Retrieved 2011-12-31.
- ↑ Fuchs, Jean-Noël; Lim, Lih-King; Montambaux, Gilles (2012). "Interband tunneling near the merging transition of Dirac cones". Physical Review A 86 (6): 063613. doi:10.1103/PhysRevA.86.063613. Bibcode: 2012PhRvA..86f3613F. https://www.equipes.lps.u-psud.fr/Montambaux/reprints/178-interband-tunneling.pdf.
- ↑ Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Katsnelson, M.I.; Grigorieva, I.V. et al. (10 Nov 2005). "Two-dimensional gas of massless Dirac fermions in graphene". Nature 438 (7065): 197–200. doi:10.1038/nature04233. PMID 16281030. Bibcode: 2005Natur.438..197N. https://www.nature.com/articles/nature04233. Retrieved 2 Mar 2018.
- ↑ "Two-dimensional Dirac materials: Structure, properties, and rarity". http://phys.org/news/2015-04-two-dimensional-dirac-materials-properties-rarity.html.
- ↑ 11.0 11.1 11.2 Hasan, M.Z.; Moore, J.E. (2011). "Three-dimensional topological insulators" (in En). Annual Review of Condensed Matter Physics 2: 55–78. doi:10.1146/annurev-conmatphys-062910-140432. Bibcode: 2011ARCMP...2...55H.
- ↑ Grüneis, A.; Attaccalite, C.; Rubio, A.; Vyalikh, D.V.; Molodtsov, S.L.; Fink, J. et al. (2009). "Angle-resolved photoemission study of the graphite intercalation compound KC8: A key to graphene". Physical Review B 80 (7): 075431. doi:10.1103/PhysRevB.80.075431. Bibcode: 2009PhRvB..80g5431G.
- ↑ Hsieh, D.; Qian, D.; Wray, L.; Xia, Y.; Hor, Y.S.; Cava, R.J.; Hasan, M.Z. (2008). "A topological Dirac insulator in a quantum spin Hall phase" (in En). Nature 452 (7190): 970–974. doi:10.1038/nature06843. ISSN 0028-0836. PMID 18432240. Bibcode: 2008Natur.452..970H.
- ↑ Hsieh, D.; Xia, Y.; Qian, D.; Wray, L.; Dil, J.H.; Meier, F. et al. (2009). "A tunable, topological insulator in the spin helical Dirac transport regime". Nature 460 (7259): 1101–1105. doi:10.1038/nature08234. PMID 19620959. Bibcode: 2009Natur.460.1101H.
- ↑ Wehling, T.O.; Black-Schaffer, A.M.; Balatsky, A.V. (2014). "Dirac materials". Advances in Physics 63 (1): 1. doi:10.1080/00018732.2014.927109. Bibcode: 2014AdPhy..63....1W.
- ↑ Singh, Bahadur; Sharma, Ashutosh; Lin, H.; Hasan, M.Z.; Prasad, R.; Bansil, A. (2012-09-18). "Topological electronic structure and Weyl semimetal in the TlBiSe2 class". Physical Review B 86 (11): 115208. doi:10.1103/PhysRevB.86.115208.
- ↑ Huang, S.-M.; Xu, S.-Y.; Belopolski, I.; Lee, C.-C.; Chang, G.; Wang, B.K. et al. (2015). "A Weyl Fermion semimetal with surface Fermi arcs in the transition metal monopnictide TaAs class". Nature Communications 6: 7373. doi:10.1038/ncomms8373. PMID 26067579. Bibcode: 2015NatCo...6.7373H.
- ↑ Weng, Hongming; Fang, Chen; Fang, Zhong; Bernevig, B. Andrei; Dai, Xi (2015). "Weyl semimetal phase in non-centrosymmetric transition-metal monophosphides". Physical Review X 5 (1): 011029. doi:10.1103/PhysRevX.5.011029. Bibcode: 2015PhRvX...5a1029W.
- ↑ Xu, S.-Y.; Belopolski, I.; Alidoust, N.; Neupane, M.; Bian, G.; Zhang, C. et al. (2015). "Discovery of a Weyl Fermion semimetal and topological Fermi arcs". Science 349 (6248): 613–617. doi:10.1126/science.aaa9297. PMID 26184916. Bibcode: 2015Sci...349..613X. https://www.science.org/doi/abs/10.1126/science.aaa9297.
- ↑ Xu, Su-Yang; Alidoust, Nasser; Belopolski, Ilya; Yuan, Zhujun; Bian, Guang; Chang, Tay-Rong et al. (2015). "Discovery of a Weyl fermion state with Fermi arcs in niobium arsenide" (in en). Nature Physics 11 (9): 748–754. doi:10.1038/nphys3437. ISSN 1745-2481. Bibcode: 2015NatPh..11..748X. https://www.nature.com/articles/nphys3437.
- ↑ Huang, Xiaochun; Zhao, Lingxiao; Long, Yujia; Wang, Peipei; Chen, Dong; Yang, Zhanhai et al. (2015). "Observation of the chiral-anomaly-induced negative magnetoresistance in 3‑D Weyl semimetal TaAs". Physical Review X 5 (3): 031023. doi:10.1103/PhysRevX.5.031023. Bibcode: 2015PhRvX...5c1023H.
- ↑ Zhang, Cheng-Long; Xu, Su-Yang; Belopolski, Ilya; Yuan, Zhujun; Lin, Ziquan; Tong, Bingbing et al. (2016-02-25). "Signatures of the Adler–Bell–Jackiw chiral anomaly in a Weyl fermion semimetal" (in en). Nature Communications 7 (1): 10735. doi:10.1038/ncomms10735. ISSN 2041-1723. PMID 26911701. Bibcode: 2016NatCo...710735Z.
- ↑ Schoop, Leslie M.; Ali, Mazhar N.; Straßer, Carola; Topp, Andreas; Varykhalov, Andrei; Marchenko, Dmitry et al. (2016). "Dirac cone protected by non-symmorphic symmetry and three-dimensional Dirac line node in ZrSiS". Nature Communications 7 (1): 11696. doi:10.1038/ncomms11696. ISSN 2041-1723. PMID 27241624. Bibcode: 2016NatCo...711696S.
- ↑ Neupane, M.; Belopolski, I.; Hosen, Md.M.; Sanchez, D.S.; Sankar, R.; Szlawska, M. et al. (2016). "Observation of topological nodal fermion semimetal phase in ZrSiS". Physical Review B 93 (20): 201104(R). doi:10.1103/PhysRevB.93.201104. ISSN 2469-9969. Bibcode: 2016PhRvB..93t1104N.
- ↑ Lu, Ling; Fu, Liang; Joannopoulos, John D.; Soljačic, Marin (17 Mar 2013). "Weyl points and line nodes in gyroid photonic crystals". Nature Photonics 7 (4): 294–299. doi:10.1038/nphoton.2013.42. Bibcode: 2013NaPho...7..294L. https://www.mit.edu/~soljacic/Weyl_nat-phot.pdf. Retrieved 2 Mar 2018.
- ↑ Neupane, Madhab; Xu, Su-Yang; Sankar, Raman; Nasser, Alidoust; Bian, Guang; Liu, Chang et al. (2014). "Observation of a three-dimensional topological Dirac semimetal phase in high-mobility Cd3As2". Nature Communications 5: 3786. doi:10.1038/ncomms4786. PMID 24807399. Bibcode: 2014NatCo...5.3786N.
- ↑ Sankar, R.; Neupane, M.; Xu, S.-Y.; Butler, C.J.; Zeljkovic, I.; Panneer Muthuselvam, I. et al. (2015). "Large single crystal growth, transport property, and spectroscopic characterizations of three-dimensional Dirac semimetal Cd3As2". Scientific Reports 5: 12966. doi:10.1038/srep12966. PMID 26272041. Bibcode: 2015NatSR...512966S.
- ↑ Borisenko, Sergey; Gibson, Quinn; Evtushinsky, Danil; Zabolotnyy, Volodymyr; Büchner, Bernd; Cava, Robert J. (2014). "Experimental realization of a three-dimensional Dirac semimetal". Physical Review Letters 113 (2): 027603. doi:10.1103/PhysRevLett.113.027603. ISSN 0031-9007. PMID 25062235. Bibcode: 2014PhRvL.113b7603B.
- ↑ Terças, H.; Flayac, H.; Solnyshkov, D. D.; Malpuech, G. (2014-02-11). "Non-Abelian Gauge Fields in Photonic Cavities and Photonic Superfluids". Physical Review Letters 112 (6): 066402. doi:10.1103/PhysRevLett.112.066402. PMID 24580697. Bibcode: 2014PhRvL.112f6402T. https://link.aps.org/doi/10.1103/PhysRevLett.112.066402.
- ↑ He, Wen-Yu; Chan, C. T. (2015-02-02). "The Emergence of Dirac points in Photonic Crystals with Mirror Symmetry" (in en). Scientific Reports 5 (1): 8186. doi:10.1038/srep08186. ISSN 2045-2322. PMID 25640993. Bibcode: 2015NatSR...5E8186H.
Further reading
- Wehling, T.O.; Black-Schaffer, A.M.; Balatsky, A.V. (2014). "Dirac materials". Advances in Physics 63 (1): 1. doi:10.1080/00018732.2014.927109. Bibcode: 2014AdPhy..63....1W.
- Johnston, Hamish (23 July 2015). "Weyl fermions are spotted at long last". http://physicsworld.com/cws/article/news/2015/jul/23/weyl-fermions-are-spotted-at-long-last.
- Ciudad, David (20 August 2015). "Massless, yet real". Nature Materials 14 (9): 863. doi:10.1038/nmat4411. ISSN 1476-1122. PMID 26288972.
- Vishwanath, Ashvin (8 September 2015). "Where the Weyl things are". Physics 8: 84. doi:10.1103/Physics.8.84. Bibcode: 2015PhyOJ...8...84V. http://physics.aps.org/articles/v8/84. Retrieved 22 November 2018.
- Jia, Shuang; Xu, Su-Yang; Hasan, M. Zahid (25 October 2016). "Weyl semimetals, Fermi arcs, and chiral anomaly". Nature Materials 15 (11): 1140–1144. doi:10.1038/nmat4787. PMID 27777402. Bibcode: 2016NatMa..15.1140J. https://www.nature.com/articles/nmat4787.
- Hasan, M. Z.; Xu, S.-Y.; Neupane, M. (2015). "Chapter 4: Topological insulators, topological Dirac semimetals, topological crystalline insulators, and topological Kondo insulators". in Ortmann, Frank; Roche, Stephan; Valenzuela, Sergio O.. Topological Insulators: Fundamentals and Perspectives. Wiley. pp. 55–100. ISBN 978-3-527-33702-6. Bibcode: 2014arXiv1406.1040Z.
 |


