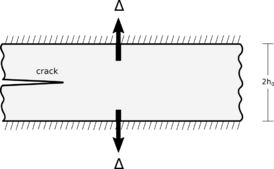Physics:Fracture of soft materials

The fracture of soft materials involves large deformations and crack blunting before propagation of the crack can occur. Consequently, the stress field close to the crack tip is significantly different from the traditional formulation encountered in the Linear elastic fracture mechanics. Therefore, fracture analysis for these applications requires a special attention. The Linear Elastic Fracture Mechanics (LEFM) and K-field (see Fracture Mechanics) are based on the assumption of infinitesimal deformation, and as a result are not suitable to describe the fracture of soft materials. However, LEFM general approach can be applied to understand the basics of fracture on soft materials. The solution for the deformation and crack stress field in soft materials considers large deformation and is derived from the finite strain elastostatics framework and hyperelastic material models.

Soft materials (Soft matter) consist of a type of material that e.g. includes soft biological tissues as well as synthetic elastomers, and that is very sensitive to thermal variations. Hence, soft materials can become highly deformed before crack propagation.

Hyperelastic material models

Hyperelastic material models are utilized to obtain the stress–strain relationship through a strain energy density function. Relevant models for deriving stress-strain relations for soft materials are: Mooney-Rivlin solid, Neo-Hookean, Exponentially hardening material and Gent hyperelastic models. On this page, the results will be primarily derived from the Neo-Hookean model.

Generalized neo-Hookean (GNH)

The Neo-Hookean model is generalized to account for the hardening factor:

[math]\displaystyle{ W = \frac{\mu}{2b} \left \{ \left[ 1 + \frac{b}{n}(I-3) \right]^{n} - 1 \right \} , }[/math]

where b>0 and n>1/2 are material parameters, and [math]\displaystyle{ I = I_{1} }[/math] is the first invariant of the Cauchy-Green deformation tensor:

[math]\displaystyle{ I_{1} = \lambda_{1}^{2}+\lambda_{2}^{2}+\lambda_{3}^{2} , }[/math]

where [math]\displaystyle{ \lambda_{\alpha} }[/math]are the principal stretches.

Specific Neo-Hookean model

Setting n=1, the specific stress-strain function for the neo-Hookean model is derived:

[math]\displaystyle{ W = \frac{\mu}{2} (I-3) }[/math].

Finite strain crack tip solutions (under large deformation)

Figure 1: Crack problem formulation. (A) Undeformed crack with coordinates ([math]\displaystyle{ x_{1},x_{2} }[/math]) in cartesian basis and ([math]\displaystyle{ r, \theta }[/math]) in polar basis. (B) Crack is under plane strain condition with uniaxial load and the coordinates are ([math]\displaystyle{ y_{1},y_{2} }[/math]) in cartesian basis and ([math]\displaystyle{ \rho,\phi }[/math]) in polar basis. Adapted from Long and Hui [4].

Since LEFM is no longer applicable, alternative methods are adapted to capture large deformations in the calculation of stress and deformation fields. In this context the method of asymptotic analysis is of relevance.

Method of asymptotic analysis

The method of asymptotic analysis consists of analyzing the crack-tip asymptotically to find a series expansion of the deformed coordinates capable to characterize the solution near the crack tip. The analysis is reducible to a nonlinear eigenvalue problem.

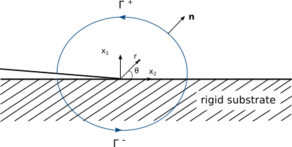
The problem is formulated based on a crack in an infinite solid, loaded at infinity with uniform uni-axial tension under condition of plane strain (see Fig.1). As the crack deforms and progresses, the coordinates in the current configuration are represented by [math]\displaystyle{ y_{1} }[/math] and [math]\displaystyle{ y_{2} }[/math] in cartesian basis and [math]\displaystyle{ \rho }[/math] and [math]\displaystyle{ \phi }[/math] in polar basis. The coordinates [math]\displaystyle{ y_{1} }[/math] and [math]\displaystyle{ y_{2} }[/math] are functions of the undeformed coordinates ([math]\displaystyle{ r, \theta }[/math]) and near the crack tip, as r→0, can be specified as:

[math]\displaystyle{ y_{\alpha}(r,\theta) = r^{m_{\alpha}} \upsilon_{\alpha}(\theta)+r^{p_{\alpha}} q_{\alpha}(\theta)+... }[/math]

[math]\displaystyle{ m_{\alpha}\lt p_{\alpha}, }[/math] [math]\displaystyle{ \alpha = 1,2 , }[/math]

where [math]\displaystyle{ m_{\alpha} }[/math], [math]\displaystyle{ p_{\alpha} }[/math] are unknown exponents, and [math]\displaystyle{ \upsilon_{\alpha}(\theta) }[/math], [math]\displaystyle{ q_{\alpha}(\theta) }[/math] are unknown functions describing the angular variation.

In order to obtain the eigenvalues, the equation above is substituted into the constitutive model, which yields the corresponding nominal stress components. Then, the stresses are substituted into the equilibrium equations (the same formulation as in LEFM theory) and the boundary conditions are applied. The most dominating terms are retained resulting in an eigenvalue problem for [math]\displaystyle{ \upsilon_{\alpha}(\theta) }[/math] and [math]\displaystyle{ m_{\alpha} }[/math].

Deformation and stress field in a plane strain crack

For the case of a homogeneous neo-Hookean solid (n=1) under Mode I condition the deformed coordinates for a plane strain configuration are given by

[math]\displaystyle{ y_{1}=-b_{0}r \sin^{2}(\theta/2), \quad y_{2}=ar^{1/2}\sin(\theta/2) , }[/math]

where a and [math]\displaystyle{ b_{0} }[/math]are unknown positive amplitudes that depends on the applied loading and specimen geometry.

The leading terms for the nominal stress (or first Piola–Kirchhoff stress, denoted by [math]\displaystyle{ \sigma }[/math] on this page) are:

[math]\displaystyle{ \sigma_{11}=\mu b_{0}, \quad \sigma_{12}=o(1) , }[/math]

[math]\displaystyle{ \sigma_{21}=-\frac{\mu a}{2} r^{-1/2}\sin(\theta/2) , }[/math]

[math]\displaystyle{ \sigma_{22}=\frac{\mu a}{2} r^{-1/2}\cos(\theta/2) . }[/math]

Thus, [math]\displaystyle{ \sigma_{11} }[/math]and [math]\displaystyle{ \sigma_{21} }[/math]are bounded at the crack tip and [math]\displaystyle{ \sigma_{21} }[/math]and [math]\displaystyle{ \sigma_{22} }[/math]have the same singularity.

The leading terms for the true stress (or Cauchy stress, denoted by [math]\displaystyle{ \tau }[/math] on this page),

[math]\displaystyle{ \tau_{11}=\mu b_{0}^{2}\sin^{2}(\theta/2) , }[/math]

[math]\displaystyle{ \tau_{12}=\tau_{21} = -\frac{\mu}{2} a b_{0} r^{-1/2} \sin^{2}(\theta/2) , }[/math]

[math]\displaystyle{ \tau_{22}=\frac{\mu}{4} a^{2} r^{-1}. }[/math]

The only true stress component completely defined by a is [math]\displaystyle{ \tau_{22} }[/math]. It also presents the most severe singularity. With that, it is clear that the singularity differs if the stress is given in the current or reference configuration. Additionally, in LEFM, the true stress field under Mode I has a singularity of [math]\displaystyle{ {r}^{-1/2} }[/math], which is weaker than the singularity in [math]\displaystyle{ \tau_{22} }[/math].

While in LEFM the near tip displacement field depends only on the Mode I stress intensity factor, it is shown here that for large deformations, the displacement depends on two parameters (a and [math]\displaystyle{ b_{0} }[/math] for a plane strain condition).

Deformation and stress field in a plane stress crack

The crack tip deformation field for a Mode I configuration in a homogeneous material neo-Hookean solid (n=1) is given by

[math]\displaystyle{ y_{1}= cr \, \cos\theta, \quad y_{2}=a\sqrt{r} \sin(\theta/2) , }[/math]

where a and c are positive independent amplitudes determined by far field boundary conditions.

The dominant terms of the nominal stress are

[math]\displaystyle{ \sigma_{11}=\mu c, \quad \sigma_{12}=o(1) , }[/math]

[math]\displaystyle{ \sigma_{21}=-\frac{\mu a}{2} r^{-1/2} \sin(\theta/2) , }[/math]

[math]\displaystyle{ \sigma_{22}=\frac{\mu a}{2} r^{-1/2} \cos(\theta/2) . }[/math]

And the true stress components are

[math]\displaystyle{ \tau_{11}=\mu c^{2}, \quad \tau_{12}=\tau_{21} = -\frac{\mu }{2} ac r^{-1/2} \sin(\theta/2) , }[/math]

[math]\displaystyle{ \tau_{22}=\frac{\mu}{4} a^{2}r^{-1}. }[/math]

Analogously, the displacement depends on two parameters (a and c for a plane stress condition) and the singularity is stronger in the [math]\displaystyle{ \tau_{22} }[/math] term.

The distribution of the true stress in the deformed coordinates (as shown in Fig. 1B) can be relevant when analyzing the crack propagation and blunt phenomenon. Additionally, it is useful when verifying experimental results of the deformation of the crack.

J-integral

The J-integral represents the energy that flows to the crack, hence, it is used to calculate the energy release rate, G. Additionally, it can be used as a fracture criterion. This integral is found to be path independent as long as the material is elastic and damages to the microstructure are not occurring.

Evaluating J on a circular path in the reference configuration yields

[math]\displaystyle{ J = \pi A \left( \frac{2n-1}{2n} \right)^{2n-1} n^{2-n} a^{2n} , }[/math]

for plane strain Mode I, where a is the amplitude of the leading order term of [math]\displaystyle{ y_2 }[/math] and A and n are material parameters from the strain-energy function.

For plane stress Mode I in a neo-Heookean material J is given by

[math]\displaystyle{ J = \frac{\mu \pi}{2} \left(\frac{b}{n} \right)^{n-1} \left( \frac{2n-1}{2n} \right)^{2n-1} n^{1-n} a^{2n} , }[/math]

where b and n are material parameters of GNH solids. For the specific case of a neo-Hookean model, where n=1, b=1 and [math]\displaystyle{ A = \mu/2 }[/math], the J-integral for plane stress and plane strain in Mode I are the same:

[math]\displaystyle{ J = \frac{\mu \pi a^{2}}{4} . }[/math]

J-integral in the pure-shear experiment

The J-integral can be determined by experiments. One common experiment is the pure-shear in an infinite long strip, as shown in Fig. 2. The upper and bottom edges are clamped by grips and the loading is applied by pulling the grips vertically apart by ± ∆. This set generates a condition of plane stress.

Figure 2: Pure-shear experiment.

Under these conditions, the J-integral is evaluated, therefore, as

[math]\displaystyle{ J = 2h_{0}W(I_{1},I_{2})=2h_{0}\Psi(\lambda) , }[/math]

where [math]\displaystyle{ I_{1}=I_{2}=\lambda^{2}+\lambda^{-2}+1 , }[/math] [math]\displaystyle{ \lambda = 1 + \frac{\Delta}{h_{0}} , }[/math]

and [math]\displaystyle{ h_{0} }[/math]is the high of the strip undeformed state. The function [math]\displaystyle{ \Psi(\lambda) }[/math]is determined by measuring the nominal stress acting on the strip stretched by [math]\displaystyle{ \lambda }[/math]:

[math]\displaystyle{ \Psi = \int_{1}^{\lambda} \sigma(\lambda) d\lambda . }[/math]

Therefore, from the imposed displacement of each grip, ± ∆, it is possible to determine the J-integral for the corresponding nominal stress. With the J-integral, the amplitude (parameter a) of some true stress components can be found. Some other stress components amplitudes, however, depend on other parameters such as c (e.g. [math]\displaystyle{ \sigma_{11} }[/math] under plane stress condition) and cannot be determined by the pure shear experiment. Nevertheless, the pure shear experiment is very important because it allows the characterization of fracture toughness of soft materials.

Interface cracks

Figure 3: Geometry of the interface crack. Adapted from Gaubelle and Knauss [5].

To approach the interaction of adhesion between soft adhesives and rigid substrates, the asymptotic solution for an interface crack problem between a GNH material and a rigid substrate is specified. The interface crack configuration considered here is shown in Fig.3 where the lateral slip is disregarded.

For the special neo-Hookean case with n=1, and [math]\displaystyle{ \overline{v_{1}}=\overline{v_{2}}=\cos \theta }[/math], the solution for the deformed coordinates is

[math]\displaystyle{ y_{1}=a_{1}r^{\frac{1}{2}} \sin\left( \frac{\theta}{2} \right) + r \cos \theta , }[/math]

[math]\displaystyle{ y_{2}=a_{2}r^{\frac{1}{2}} \sin\left( \frac{\theta}{2} \right), }[/math]

Figure 4: Soft material and rigid substrate interface. A) Plot of the crack tip deformed coordinates. B) Parabolic shape of the crack tip.

which is equivalent to

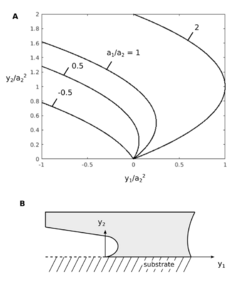
[math]\displaystyle{ y_{1} = \frac{a_{1}}{a_{2}}y_{2}-\left( \frac{y_{2}}{a_{2}} \right)^{2} . }[/math]

According to the above equation, the crack on this type of interface is found to open with a parabolic shape. This is confirmed by plotting the normalized coordinates [math]\displaystyle{ y_{1}/a_{2}^2 }[/math] vs [math]\displaystyle{ y_{2}/a_{2}^{2} }[/math] for different [math]\displaystyle{ a_{1}/a_{2} }[/math] ratios (see Fig. 4).

To go through the analysis of the interface between two GNH sheets with the same hardening characteristics, refer to the model described by Gaubelle and Knauss.

See also

• Fracture mechanics
• Soft matter
• J-integral
• Neo-Hookean solid
• Gent (hyperelastic model)
• Mooney-rivlin solid
• Fracture of Biological Materials