Physics:Fundamental series
The fundamental series is a set of spectral lines in a set caused by transition between d and f orbitals in atoms.
Originally the series was discovered in the infrared by Fowler and independently by Arno Bergmann.[1] This resulted in the name Bergmann series used for such a set of lines in a spectrum. However the name was changed as Bergmann also discovered other series of lines. And other discoverers also established other such series. They became known as the fundamental series.[2] Bergmann observed lithium at 5347 cm−1, sodium at 5416 cm−1 potassium at 6592 cm−1.[2] Bergmann observed that the lines in the series in the caesium spectrum were double. His discovery was announced in Contributions to the Knowledge of the Infra-Red Emission Spectra of the Alkalies, Jena 1907.[3] Carl Runge called this series the "new series". He predicted that the lines of potassium and rubidium would be in pairs.[3] He expressed the frequencies of the series lines by a formula and predicted a connection of the series limit to the other known series. In 1909 W. M. Hicks produced approximate formulas for the various series and noticed that this series had a simpler formula than the others and thus called it the "fundamental series" and used the letter F.[1][4]
The formula that more resembled the hydrogen spectrum calculations was because of a smaller quantum defect. There is no physical basis to call this fundamental.[5] The fundamental series was described as badly-named.[6] It is the last spectroscopic series to have a special designation.[6] The next series involving transitions between F and G subshells is known as the FG series.[6]
Frequencies of the lines in the series are given by this formula:
[math]\displaystyle{ \nu = \frac{R}{\left[ 3+d\right]^2}-\frac{R}{\left[ m+f\right]^2} \text{, with } m=4,5,6,..., }[/math]
R is the Rydberg constant, [math]\displaystyle{ T_{BS}=\frac{R}{\left[ 3+d\right]^2} }[/math] is the series limit, represented by 3D, and [math]\displaystyle{ \frac{R}{\left[ m+f\right]^2} }[/math] is represented by mF. A shortened formula is then given by [math]\displaystyle{ \nu=3D-mF }[/math] with values of m being integers from 4 upwards.[7] The two numbers separated by the "−" are called terms, that represent the energy level of an atom.
The limit of the fundamental series is the same as the 3D level.[5]
The terms can have different designations, mF for single line systems, mΦ for doublets and mf for triplets.[8]
Lines in the fundamental series are split into compound doublets, due to the D and F subshells having different spin possibilities. The splitting of the D subshell is very small and that of the F subshell even less so, so the fine structure in the fundamental series is harder to resolve than that in the sharp or diffuse series.[7]
Lithium
The quantum defect for lithium is 0.[5]
Sodium
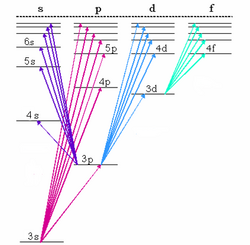
The fundamental series lines for sodium appear in the near infrared.
| sodium fundamental series[9] | ||
|---|---|---|
| transition | wavelength 1 Å | |
| 3d-4f | 18465.3 | |
| 3d-5f | 12679.2 | |
| 3d-6f | 10834.9 | |
| 3d-7f | 9961.28 | |
| 3d-8f | 9465.94 | |
| 3d-9f | 9153.88 | |
| 3d-10f | 8942.96 | |
| 3d-11f | 8796 | |
Potassium
The fundamental series lines for potassium appear in the near infrared.
| potassium fundamental series[10] | ||
|---|---|---|
| transition | wavelength 1 Å | wavelength 2 Å |
| 3d-4f | 15163.1 | 15168.4 |
| 3d-5f | 11022.3 | |
| 3d-6f | 9565.6 | 9597.76 |
| 3d-7f | 8902.2 | 8902.4 |
| 3d-8f | 8503.5 | 8505.3 |
| 3d-9f | 8250.2 | 8251.7 |
Rubidium
The fundamental series lines for rubidium appear in the near infrared. The valence electron moves from the 4d level as the 3d is contained in an inner shell. They were observed by R von Lamb. Relevant energy levels are 4p64d j=5/2 19,355.282 cm−1 and j=3/2 19,355.623 cm−1, and the first f levels at 4p64f j=5/2 26,792.185 cm−1 and j=7/2 26,792.169 cm−1.[11]
| rubidium fundamental series[11] | ||
|---|---|---|
| transition | vacuum wavelength 1 Å 5/2–7/2 | vacuum wavelength 2 Å 3/2-5/2 |
| 4d-4f | 13,446.486 | 13,447.076 |
| 4d-5f | 10,078.039 | 10,078.473 |
| 4d-6f | 8870.943 | 8871.281 |
| 4d-7f | 8273.684 | 8273.981 |
| 4d-8f | 7927.440 | |
Caesium
| caesium fundamental series[12] | |||
|---|---|---|---|
| transition | wavelengths Å | ||
| 5/2–7/2 | 5/2-5/2 | 3/2-5/2 | |
| 5d-4f | 10,126.376 7 | 10,126.188 | 10,027.103 3 |
| 5d-5f | 8,079.036 3 | 8,078.936 | 8,015.726 3 |
| 5d-6f | 7,279.956 8 | 7,279.889 | 7,228.533 6 |
| 5d-7f | 6,870.454 4 | 6,824.651 3 | |
| 5d-8f | 6,628.657 6 | 6,586.021 6 | |
| 5d-9f | 6,472.619 6 | 6,431.966 2 | |
| 5d-10f | 6,365.522 6 | 6,326.203 4 | |
| 5d-11f | 6,288.592 7 | 6,250.214 9 | |
| 5d-12f | 6,231.349 0 | 6,193.668 9 | |
| 5d-13f | 6,187.544 2 | 6,150.38 | |
| 5d-14f | 6,153.238 1 | 6,116.52 | |
References
- ↑ 1.0 1.1 Saunders, F. A. (August 1919). "Review of Recent Work on the Series Spectra of Helium and of Hydrogen". Astrophysical Journal 50: 151. doi:10.1086/142490. Bibcode: 1919ApJ....50..151S.
- ↑ 2.0 2.1 Brand, J. C. D. (24 Nov 1995). Lines of Light. CRC Press. p. 135. ISBN 9782884491631. https://books.google.com/books?id=sKx0IBC22p4C&pg=PA135.
- ↑ 3.0 3.1 Runge, Carl (December 1907). "The Spectra of the Alkalies". Astrophysical Journal 27: 158–160. doi:10.1086/141538. Bibcode: 1908ApJ....27..158R.
- ↑ Hicks, W. M. (9 December 1909). "A Critical Study of Spectral Series.-Part I. The Alkalies H and He". Philosophical Transactions of the Royal Society of London A 210 (459–470): 57–111. doi:10.1098/rsta.1911.0003.
- ↑ 5.0 5.1 5.2 Candler, A. C. (1937). Atomic Spectra and the Vector Model: Volume 1. Cambridge, UK: Cambridge University Press. p. 22. ISBN 9781001286228. https://books.google.com/books?id=SWw3AAAAIAAJ&pg=PA22. Retrieved 28 August 2015.
- ↑ 6.0 6.1 6.2 Fowler, A. (23 February 1928). "Spectra and atoms". Journal of the Chemical Society (Resumed): 764–780. doi:10.1039/JR9280000764. http://pubs.rsc.org/en/content/articlelanding/1928/jr/jr9280000764. (Subscription content?)
- ↑ 7.0 7.1 Herzberg, Gerhard (January 1944). Atomic Spectra and Atomic Structure. Courier Corporation. p. 56. ISBN 9780486601151. https://archive.org/details/in.ernet.dli.2015.202294.
- ↑ Saunders, F. A. (1915). "Some Recent Discoveries in Spectrum Series". Astrophysical Journal 41: 323. doi:10.1086/142175. Bibcode: 1915ApJ....41..323S.
- ↑ Wiese, W.; Smith, M. W.; Miles, B. M. (October 1969). Atomic Transition Probabilities Volume II Sodium Through Calcium A Critical Data Compilation. Washington: National Bureau of Standards. pp. 39–41. http://www.dtic.mil/dtic/tr/fulltext/u2/696884.pdf.
- ↑ Wiese, W.; Smith, M. W.; Miles, B. M. (October 1969). Atomic Transition Probabilities Volume II Sodium Through Calcium A Critical Data Compilation. Washington: National Bureau of Standards. pp. 228–229. http://www.dtic.mil/dtic/tr/fulltext/u2/696884.pdf.
- ↑ 11.0 11.1 Luna, F.R.T.; Cavalcanti, G.H.; Coutinho, L.H.; Trigueiros, A.G. (December 2002). "A compilation of wavelengths and energy levels for the spectrum of neutral rubidium (RbI)". Journal of Quantitative Spectroscopy and Radiative Transfer 75 (5): 559–587. doi:10.1016/S0022-4073(02)00030-4. Bibcode: 2002JQSRT..75..559L. (Subscription content?)
- ↑ Sansonetti, Jean E. (2009). "Wavelengths, Transition Probabilities, and Energy Levels for the Spectra of Cesium (Cs I–Cs LV)". Journal of Physical and Chemical Reference Data 38 (4): 768–769. doi:10.1063/1.3132702. Bibcode: 2009JPCRD..38..761S. http://129.6.13.54/srd/upload/jpcrd382009761p.pdf. Retrieved 25 August 2015.
 |

