Physics:Non-random two-liquid model
The non-random two-liquid model[1] (abbreviated NRTL model) is an activity coefficient model that correlates the activity coefficients [math]\displaystyle{ \gamma_i }[/math] of a compound with its mole fractions [math]\displaystyle{ x_i }[/math] in the liquid phase concerned. It is frequently applied in the field of chemical engineering to calculate phase equilibria. The concept of NRTL is based on the hypothesis of Wilson that the local concentration around a molecule is different from the bulk concentration. This difference is due to a difference between the interaction energy of the central molecule with the molecules of its own kind [math]\displaystyle{ U_{ii} }[/math] and that with the molecules of the other kind [math]\displaystyle{ U_{ij} }[/math]. The energy difference also introduces a non-randomness at the local molecular level. The NRTL model belongs to the so-called local-composition models. Other models of this type are the Wilson model, the UNIQUAC model, and the group contribution model UNIFAC. These local-composition models are not thermodynamically consistent for a one-fluid model for a real mixture due to the assumption that the local composition around molecule i is independent of the local composition around molecule j. This assumption is not true, as was shown by Flemr in 1976.[2] However, they are consistent if a hypothetical two-liquid model is used.[3]
Derivation
Like Wilson (1964), Renon & Prausnitz (1968) began with local composition theory,[4] but instead of using the Flory–Huggins volumetric expression as Wilson did, they assumed local compositions followed
- [math]\displaystyle{ \frac{x_{21}}{x_{11}} = \frac{x_2}{x_1} \frac{\exp(-\alpha_{21} g_{21}/RT)}{\exp(-\alpha_{11} g_{11}/RT)} }[/math]
with a new "non-randomness" parameter α. The excess Gibbs free energy was then determined to be
- [math]\displaystyle{ \frac{G^{ex}}{RT} = \sum_i^N x_i \frac{\sum_j^N \tau_{ji} G_{ji} x_j}{\sum_k^N G_{ki} x_k} }[/math].
Unlike Wilson's equation, this can predict partially miscible mixtures. However, the cross term, like Wohl's expansion, is more suitable for [math]\displaystyle{ H^\text{ex} }[/math] than [math]\displaystyle{ G^\text{ex} }[/math], and experimental data is not always sufficiently plentiful to yield three meaningful values, so later attempts to extend Wilson's equation to partial miscibility (or to extend Guggenheim's quasichemical theory for nonrandom mixtures to Wilson's different-sized molecules) eventually yielded variants like UNIQUAC.
Equations for a binary mixture
For a binary mixture the following function[5] are used:
- [math]\displaystyle{ \left\{\begin{matrix} \ln\ \gamma_1=x^2_2\left[\tau_{21}\left(\frac{G_{21}}{x_1+x_2 G_{21}}\right)^2 +\frac{\tau_{12} G_{12}} {(x_2+x_1 G_{12})^2 }\right] \\ \\ \ln\ \gamma_2=x^2_1\left[\tau_{12}\left(\frac{G_{12}}{x_2+x_1 G_{12}}\right)^2 +\frac{\tau_{21} G_{21}} {(x_1+x_2 G_{21})^2 }\right] \end{matrix}\right. }[/math]
with
- [math]\displaystyle{ \left\{\begin{matrix} \ln\ G_{12}=-\alpha_{12}\ \tau_{12} \\ \ln\ G_{21}=-\alpha_{21}\ \tau_{21} \end{matrix}\right. }[/math]
Here, [math]\displaystyle{ \tau_{12} }[/math] and [math]\displaystyle{ \tau_{21} }[/math] are the dimensionless interaction parameters, which are related to the interaction energy parameters [math]\displaystyle{ \Delta g_{12} }[/math] and [math]\displaystyle{ \Delta g_{21} }[/math] by:
- [math]\displaystyle{ \left\{\begin{matrix} \tau_{12}=\frac{\Delta g_{12}}{RT}=\frac{U_{12}-U_{22}}{RT} \\ \tau_{21}=\frac{\Delta g_{21}}{RT}=\frac{U_{21}-U_{11}}{RT} \end{matrix}\right. }[/math]
Here R is the gas constant and T the absolute temperature, and Uij is the energy between molecular surface i and j. Uii is the energy of evaporation. Here Uij has to be equal to Uji, but [math]\displaystyle{ \Delta g_{ij} }[/math] is not necessary equal to [math]\displaystyle{ \Delta g_{ji} }[/math].
The parameters [math]\displaystyle{ \alpha_{12} }[/math] and [math]\displaystyle{ \alpha_{21} }[/math] are the so-called non-randomness parameter, for which usually [math]\displaystyle{ \alpha_{12} }[/math] is set equal to [math]\displaystyle{ \alpha_{21} }[/math]. For a liquid, in which the local distribution is random around the center molecule, the parameter [math]\displaystyle{ \alpha_{12}=0 }[/math]. In that case the equations reduce to the one-parameter Margules activity model:
- [math]\displaystyle{ \left\{\begin{matrix} \ln\ \gamma_1=x^2_2\left[\tau_{21} +\tau_{12} \right]=Ax^2_2 \\ \ln\ \gamma_2=x^2_1\left[\tau_{12}+\tau_{21} \right]=Ax^2_1 \end{matrix}\right. }[/math]
In practice, [math]\displaystyle{ \alpha_{12} }[/math] is set to 0.2, 0.3 or 0.48. The latter value is frequently used for aqueous systems. The high value reflects the ordered structure caused by hydrogen bonds. However, in the description of liquid-liquid equilibria the non-randomness parameter is set to 0.2 to avoid wrong liquid-liquid description. In some cases a better phase equilibria description is obtained by setting [math]\displaystyle{ \alpha_{12}=-1 }[/math].[6] However this mathematical solution is impossible from a physical point of view, since no system can be more random than random ([math]\displaystyle{ \alpha_{12} }[/math] =0). In general NRTL offers more flexibility in the description of phase equilibria than other activity models due to the extra non-randomness parameters. However, in practice this flexibility is reduced in order to avoid wrong equilibrium description outside the range of regressed data.
The limiting activity coefficients, also known as the activity coefficients at infinite dilution, are calculated by:
- [math]\displaystyle{ \left\{\begin{matrix} \ln\ \gamma_1^\infty=\left[\tau_{21} +\tau_{12} \exp{(-\alpha_{12}\ \tau_{12})} \right] \\ \ln\ \gamma_2^\infty=\left[\tau_{12} +\tau_{21}\exp{(-\alpha_{12}\ \tau_{21})}\right] \end{matrix}\right. }[/math]
The expressions show that at [math]\displaystyle{ \alpha_{12}=0 }[/math] the limiting activity coefficients are equal. This situation that occurs for molecules of equal size, but of different polarities.
It also shows, since three parameters are available, that multiple sets of solutions are possible.
General equations
The general equation for [math]\displaystyle{ \ln(\gamma_i) }[/math] for species [math]\displaystyle{ i }[/math] in a mixture of [math]\displaystyle{ n }[/math] components is:[7]
- [math]\displaystyle{ \ln(\gamma_i)=\frac{\displaystyle\sum_{j=1}^{n}{x_{j}\tau_{ji}G_{ji}}}{\displaystyle\sum_{k=1}^{n}{x_{k}G_{ki}}}+\sum_{j=1}^{n}{\frac{x_{j}G_{ij}}{\displaystyle\sum_{k=1}^{n}{x_{k}G_{kj}}}}{\left ({\tau_{ij}-\frac{\displaystyle\sum_{m=1}^{n}{x_{m}\tau_{mj}G_{mj}}}{\displaystyle\sum_{k=1}^{n}{x_{k}G_{kj}}}}\right )} }[/math]
with
- [math]\displaystyle{ G_{ij}=\exp\left ({-\alpha_{ij}\tau_{ij}}\right ) }[/math]
- [math]\displaystyle{ \alpha_{ij}=\alpha_{ij_{0}}+\alpha_{ij_{1}}T }[/math]
- [math]\displaystyle{ \tau_{i,j}=A_{ij}+\frac{B_{ij}}{T}+\frac{C_{ij}}{T^{2}}+D_{ij}\ln{\left ({T}\right )}+E_{ij}T^{F_{ij}} }[/math]
There are several different equation forms for [math]\displaystyle{ \alpha_{ij} }[/math] and [math]\displaystyle{ \tau_{ij} }[/math], the most general of which are shown above.
Temperature dependent parameters
To describe phase equilibria over a large temperature regime, i.e. larger than 50 K, the interaction parameter has to be made temperature dependent. Two formats are frequently used. The extended Antoine equation format:
- [math]\displaystyle{ \tau_{ij}=f(T)=a_{ij}+\frac{b_{ij}}{T}+c_{ij}\ \ln\ T+d_{ij}T }[/math]
Here the logarithmic and linear terms are mainly used in the description of liquid-liquid equilibria (miscibility gap).
The other format is a second-order polynomial format:
- [math]\displaystyle{ \Delta g_{ij}=f(T)=a_{ij}+b_{ij}\cdot T +c_{ij}T^{2} }[/math]
Parameter determination
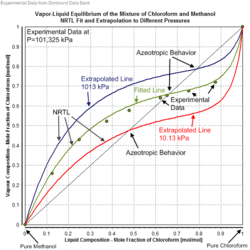
The NRTL parameters are fitted to activity coefficients that have been derived from experimentally determined phase equilibrium data (vapor–liquid, liquid–liquid, solid–liquid) as well as from heats of mixing. The source of the experimental data are often factual data banks like the Dortmund Data Bank. Other options are direct experimental work and predicted activity coefficients with UNIFAC and similar models. Noteworthy is that for the same liquid mixture several NRTL parameter sets might exist. The NRTL parameter set to use depends on the kind of phase equilibrium (i.e. solid–liquid (SL), liquid–liquid (LL), vapor–liquid (VL)). In the case of the description of a vapor–liquid equilibria it is necessary to know which saturated vapor pressure of the pure components was used and whether the gas phase was treated as an ideal or a real gas. Accurate saturated vapor pressure values are important in the determination or the description of an azeotrope. The gas fugacity coefficients are mostly set to unity (ideal gas assumption), but for vapor-liquid equilibria at high pressures (i.e. > 10 bar) an equation of state is needed to calculate the gas fugacity coefficient for a real gas description.
Determination of NRTL parameters from LLE data is more complicated than parameter regression from VLE data as it involves solving isoactivity equations which are highly non-linear. In addition, parameters obtained from LLE may not always represent the real activity of components due to lack of knowledge on the activity values of components in the data regression.[8][9][10] For this reason it is necessary to confirm the consistency of the obtained parameters in the whole range of compositions (including binary subsystems, experimental and calculated lie-lines, Hessian matrix, etc.).[11][12][13]
Literature
- ↑ Renon H., Prausnitz J. M., "Local Compositions in Thermodynamic Excess Functions for Liquid Mixtures", AIChE J., 14(1), S.135–144, 1968
- ↑ McDermott (Fluid Phase Equilibrium 1(1977)33) and Flemr (Coll. Czech. Chem.Comm., 41 (1976) 3347)
- ↑ Hu, Y.; Azevedo, E.G.; Prausnitz, J.M. (1983). "The molecular basis for local compositions in liquid mixture models". Fluid Phase Equilibria 13: 351–360. doi:10.1016/0378-3812(83)80106-X. https://escholarship.org/uc/item/3x693561.
- ↑ Renon, Henri; Prausnitz, J. M. (1968). "Local compositions in thermodynamic excess functions for liquid mixtures" (in en). AIChE Journal 14 (1): 135–144. doi:10.1002/aic.690140124. ISSN 1547-5905.
- ↑ Reid R. C., Prausnitz J. M., Poling B. E., The Properties of Gases & Liquids, 4th Edition, McGraw-Hill, 1988
- ↑ Effective Local Compositions in Phase Equilibrium Correlations, J. M. Marina, D. P. Tassios Ind. Eng. Chem. Process Des. Dev., 1973, 12 (1), pp 67–71
- ↑ "A Property Methods and Calculations". Rowan University. http://users.rowan.edu/~hesketh/0906-316/Handouts/Pages%20from%20SimBasis%20appendix%20A%20property%20packages.pdf.
- ↑ Reyes-Labarta, J.A.; Olaya, M.M.; Velasco, R.; Serrano, M.D.; Marcilla, A. (2009). "Correlation of the Liquid-Liquid Equilibrium Data for Specific Ternary Systems with One or Two Partially Miscible Binary Subsystems". Fluid Phase Equilibria 278 (1–2): 9–14. doi:10.1016/j.fluid.2008.12.002.
- ↑ Marcilla, A.; Reyes-Labarta, J.A.; Serrano, M.D.; Olaya, M.M. (2011). "GE Models and Algorithms for Condensed Phase Equilibrium Data Regression in Ternary Systems: Limitations and Proposals". The Open Thermodynamics Journal 5: 48–62. doi:10.2174/1874396X01105010048.
- ↑ Marcilla, A.; Serrano, M.D.; Reyes-Labarta, J.A.; Olaya, M.M. (2012). "Checking Liquid-Liquid Critical Point Conditions and their Application in Ternary Systems". Industrial & Engineering Chemistry Research 51 (13): 5098–5102. doi:10.1021/ie202793r.
- ↑ Li, Z.; Smith, K. H.; Mumford, K. A.; Wang, Y.; Stevens, G. W., Regression of NRTL parameters from ternary liquid–liquid equilibria using particle swarm optimization and discussions. Fluid Phase Equilib. 2015, 398, 36-45.
- ↑ Marcilla, Antonio; Reyes-Labarta, Juan A.; Olaya, M.Mar (2017). "Should we trust all the published LLE correlation parameters in phase equilibria? Necessity of their Assessment Prior to Publication". Fluid Phase Equilibria 433: 243–252. doi:10.1016/j.fluid.2016.11.009.
- ↑ Reyes-Labarta, Juan A.; Olaya, Maria del Mar; Marcilla, Antonio (2015-11-27). Graphical User Interface (GUI) for the analysis of Gibbs Energy surfaces, including LL tie-lines and Hessian matrix. University of Alicante.
 |

