Earth:Local tangent plane coordinates
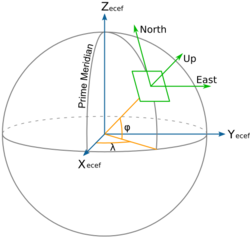
Local tangent plane coordinates (LTP), also known as local ellipsoidal system,[1][2] local geodetic coordinate system,[3] or local vertical, local horizontal coordinates (LVLH), are a spatial reference system based on the tangent plane defined by the local vertical direction and the Earth's axis of rotation. It consists of three coordinates: one represents the position along the northern axis, one along the local eastern axis, and one represents the vertical position. Two right-handed variants exist: east, north, up (ENU) coordinates and north, east, down (NED) coordinates. They serve for representing state vectors that are commonly used in aviation and marine cybernetics.
Axes
These frames are location dependent. For movements around the globe, like air or sea navigation, the frames are defined as tangent to the lines of geographical coordinates:
- East–west tangent to parallels,
- North–south tangent to meridians, and
- Up–down in the direction normal to the oblate spheroid used as Earth's ellipsoid, which does not generally pass through the center of Earth.
Local east, north, up (ENU) coordinates
In many targeting and tracking applications the local East, North, Up (ENU) Cartesian coordinate system is far more intuitive and practical than ECEF or Geodetic coordinates. The local ENU coordinates are formed from a plane tangent to the Earth's surface fixed to a specific location and hence it is sometimes known as a "Local Tangent" or "local geodetic" plane. By convention the east axis is labeled [math]\displaystyle{ x }[/math], the north [math]\displaystyle{ y }[/math] and the up [math]\displaystyle{ z }[/math].
Local north, east, down (NED) coordinates
In an airplane, most objects of interest are below the aircraft, so it is sensible to define down as a positive number. The North, East, Down (NED) coordinates allow this as an alternative to the ENU. By convention, the north axis is labeled [math]\displaystyle{ x' }[/math], the east [math]\displaystyle{ y' }[/math] and the down [math]\displaystyle{ z' }[/math]. To avoid confusion between [math]\displaystyle{ x }[/math] and [math]\displaystyle{ x' }[/math], etc. in this article we will restrict the local coordinate frame to ENU.
The origin of this coordinate system is usually chosen to be a fixed point on the surface of the geoid below the aircraft's center of gravity. When that is the case, the coordinate system is sometimes referred as a "local-North-East-Down Coordinate System".[4]
NED coordinates are similar to ECEF in that they're Cartesian, however they can be more convenient due to the relatively small numbers involved, and also because of the intuitive axes. NED and ECEF coordinates can be related with the following formula:
- [math]\displaystyle{ \mathbf p_{\mathrm{NED}} = R (\mathbf p_{\mathrm{ECEF}} - \mathbf p_{\mathrm{Ref}}) }[/math]
where [math]\displaystyle{ \mathbf p_{\mathrm{NED}} }[/math] is a 3D position in a NED system, [math]\displaystyle{ \mathbf p_{\mathrm{ECEF}} }[/math] is the corresponding ECEF position, [math]\displaystyle{ \mathbf p_{\mathrm{Ref}} }[/math] is the reference ECEF position (where the local tangent plane originates), and [math]\displaystyle{ R }[/math] is a rotation matrix whose rows are the north, east, and down axes. [math]\displaystyle{ R }[/math] may be defined conveniently from the latitude [math]\displaystyle{ \phi }[/math] and longitude [math]\displaystyle{ \lambda }[/math] corresponding to [math]\displaystyle{ \mathbf p_{\mathrm{Ref}} }[/math]:
- [math]\displaystyle{ R = \begin{bmatrix} -\sin(\phi) \cos(\lambda) & -\sin(\phi)\sin(\lambda) & \cos(\phi) \\ -\sin(\lambda) & \cos(\lambda) & 0 \\ -\cos(\phi)\cos(\lambda) & -\cos(\phi)\sin(\lambda) & -\sin(\phi) \end{bmatrix} }[/math][5]
See also
- Axes conventions
- Figure of Earth
- Horizontal coordinate system
- Geodetic coordinates
- Geodetic system
- Grid reference system
- Local coordinates
References
- ↑ Torge, Wolfgang; Müller, Jürgen (2012-05-29). Geodesy. DE GRUYTER. doi:10.1515/9783110250008. ISBN 978-3-11-020718-7.
- ↑ Seeber, Günter (2003-06-19). Satellite Geodesy. Walter de Gruyter. doi:10.1515/9783110200089. ISBN 978-3-11-017549-3.
- ↑ "Geodesy". GPS Satellite Surveying. Hoboken, NJ, USA: John Wiley & Sons, Inc. 2015-04-11. pp. 129–206. doi:10.1002/9781119018612.ch4. ISBN 978-1-119-01861-2.
- ↑ Cai, Guowei; Chen, Ben M.; Lee, Tong Heng (2011). Unmanned Rotorcraft Systems. Springer. pp. 27. ISBN 978-0-85729-634-4. https://archive.org/details/unmannedrotorcra00caig.
- ↑ Cai, Guowei; Chen, Ben M.; Lee, Tong Heng (2011). Unmanned Rotorcraft Systems. Springer. pp. 32. ISBN 978-0-85729-634-4. https://archive.org/details/unmannedrotorcra00caig.
 |