Earth:Stream order
The stream order or waterbody order is a positive whole number used in geomorphology and hydrology to indicate the level of branching in a river system.
There are various approaches[1] to the topological ordering of rivers or sections of rivers based on their distance from the source ("top down"[2]) or from the confluence (the point where two rivers merge) or river mouth ("bottom up"[3]), and their hierarchical position within the river system. As terminology, the words "stream" and "branch" tend to be used rather than "river".
Classic stream order
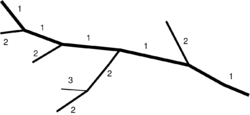
The classic stream order, also called Hack's stream order or Gravelius' stream order, is a "bottom up" hierarchy that allocates the number "1" to the river with its mouth at the sea (the main stem). Stream order is an important aspect of a drainage basin. It is defined as the measure of the position of a stream in the hierarchy of streams. Tributaries are given a number one greater than that of the river or stream into which they discharge. So, for example, all immediate tributaries of the main stem are given the number "2". Tributaries emptying into a "2" are given the number "3" and so on.[4]
This type of stream order indicates the river's place in the network. It is suitable for general cartographic purposes, but can pose problems because at each confluence, a decision must be made about which of the two branches is a continuation of the main channel, and whether the main channel has its source at the confluence of two other smaller streams. The first order stream is the one which, at each confluence, has the greatest volumetric flow, usually reflecting the long-standing naming of rivers. Associated with this stream order system was the quest by geographers of the 19th century to find the "true" source of a river. In the course of this work, other criteria were discussed to enable the main stream to be defined. In addition to measuring the length of rivers (the distance between the farthest source and the mouth) and the size of the various catchments, geographers searched for the stream which deviated least at the actual confluence, as well as taking into account the successive names of rivers and their tributaries, such as the Rhine and the Aare or the Elbe and the Vltava.
Strahler stream order
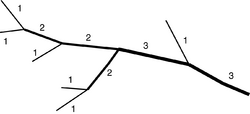
According to the "top down" system devised by Strahler, rivers of the first order are the outermost tributaries. If two streams of the same order merge, the resulting stream is given a number that is one higher. If two rivers with different stream orders merge, the resulting stream is given the higher of the two numbers.[5][6]
The Strahler order is designed to reflect the morphology of a catchment and forms the basis of important hydrographical indicators of its structure, such as its bifurcation ratio, drainage density and frequency. Its basis is the watershed line of the catchment. It is, however, scale-dependent. The larger the map scale, the more orders of stream may be revealed. A general lower boundary for the definition of a "stream" may be set by defining its width at the mouth or, referencing a map, by limiting its extent. The system itself is also applicable for other small-scale structures outside of hydrology.
Shreve stream order
The Shreve system also gives the outermost tributaries the number "1". Unlike the Strahler method, at a confluence the two numbers are added together.[7]
Shreve stream order is preferred in hydrodynamics: it sums the number of sources in each catchment above a stream gauge or outflow, and correlates roughly to the discharge volumes and pollution levels. Like the Strahler method, it is dependent on the precision of the sources included, but less dependent on map scale. It can be made relatively scale-independent by using suitable normalization and is then largely independent of an exact knowledge of the upper and lower courses of an area.[7]
Horton and topological stream orders
Other systems include the Horton stream order, an early top down system devised by Robert E. Horton,[8] and the topological stream order system, which is "a bottom up" system, and where the stream order number increases by one at every confluence.[4]
Comparison of classic stream order with Horton and Strahler methods
Classical or topological ordering systems are assigned a dimensionless numerical order of "one", starting at the mouth of a stream, which is its lowest elevation point. The vector order then increases as it traces upstream and converges with other smaller streams, resulting in a correlation of higher-order numbers to more highly elevated headwaters.
Horton proposed to establish a reversal of that order. Horton's 1947 research report established a stream ordering method based on vector geometry. In 1952, Arthur Strahler proposed a modification to Horton's method. Both Horton's and Strahler's methods established the assignment of the lowest order, number 1, starting at the river's headwater, which is the highest elevation point. Classical order number assignment correlates to height and elevation and traces upstream, but Horton and Strahler's stream ordering methods correlate to gravity flow and trace downstream.
Both Horton's and Strahler's stream ordering methods rely on principles of vector point-line geometry. Horton's and Strahler's rules form the basis of programming algorithms that interpret map data as queried by Geographic Information Systems.
Usage
The classic use of stream order is in general hydrological cartography. Stream order systems are also important for the systematic mapping of a river system, enabling the clear labelling and ordering of streams.
The Strahler and Shreve methods are particularly valuable for the modelling and morphometric analysis of river systems, because they define each section of a river. That allows the network to be separated at each gauge or outflow into upstream and downstream regimes, and for these points to be classified. These systems are also used as a basis for modelling the water budget using storage models or time-related, precipitation-outflow models and the like.
In the GIS-based earth sciences these two models are used because they show the graphical extent of a river object.
Research activity following Strahler's 1952 report has focused on solving some challenges when converting two-dimensional maps into three-dimensional vector models. One challenge has been to convert rasterized pixel images of streams into vector format. Another problem has been that map scaling adjustments when using GIS may alter the stream classification by a factor or one or two orders. Depending on the scale of the GIS map, some fine detail of the tree structure of a river system can be lost.
Research efforts by private industry, universities and federal government agencies such as the EPA and USGS have combined resources and aligned focus to study these and other challenges. The principal intent is to standardize software and programming rules so GIS data is consistently reliable at any map scale. To this end, both the EPA and USGS have spearheaded standardization efforts, culminating in the creation of The National Map. Both federal agencies, as well as leading private industry software companies have adopted Horton's and Strahler's stream order vector principles as the basis for coding logic rules built into the standardized National Map software.
See also
References
Sources
- Drwal, J. Wykształcenie i organizacja sieci hydrograficznej jako podstawa oceny struktury odpływu na terenach młodoglacjalnych, Rozprawy i monografie, Gdansk, 1982, 130 pp (in Polish)
- Hack, J. Studies of longitudinal stream profiles in Virginia and Maryland, U.S. Geological Survey Professional Paper, 1957, 294-B
- Horton, R. E., Erosional development of streams and their drainage basins: hydro-physical approach to quantitative morphology, Geological Society of America Bulletin 56 (3): 275–370, 1945
- Koschitzki, Thomas. GIS-basierte, automatische Erfassung natürlicher Fließgewässerhierarchien und ihre Abbildung in Datenbanken, beispielhaft dargestellt am Einzugsgebiet der Salza. Dissertation, Martin-Luther-Universität Halle-Wittenberg, Halle (Saale), 2004, URN (NBN) urn:nbn:de:gbv:3-000007179 (Weblink, archive server DNB)
- Scheidegger A. E., (1966), Statistical Description of River Networks. Water Resour. Res., 2(4): 785-790
- Shreve, R., (1966), Statistical Law of Stream Numbers, J. Geol., 74, 17–37.
- Strahler, A.N. Dynamic basis of geomorphology. In: Geological Society of America Bulletin 63/1952, pp. 923–938.
- Strahler, A.N. Quantitative analysis of watershed geomorphology. Transactions of the American Geophysical Union. 1957; 38(6), pp. 913-920.
- Strahler, A.N. "Quantitative geomorphology of drainage basins and channel networks." Chow, V.T., Editor. Handbook of Applied Hydrology. New York: McGraw-Hill; 1964; pp. 4-39, 4-76.
- Shreve, R. Statistical law of stream numbers. In: Journal of Geology 74/1966.
- Weishar, Lee L. Development of Marsh Hydrogeomorphology and Marsh Vegetation with a Salt Hay Farm Wetland Restoration Site. Retrieved 16 Apr 2017.
- Woldenberg, M. J., (1967), Geography and properties of surfaces, Harvard Papers in Theoretical Geography, 1: 95-189.
- Rivertool – Extension für ArcView, usages documentation, Office of Applied Hydrology (Weblink, gis-tools.de)
External links
- International Glossary of Hydrology (pdf file; 1.24 MB)
- "Gewässernetz: Stream Order Numbers for the Digitised Water Network, 1:25,000 series, Switzerland" (in German). Bundesamt für Umwelt BAFU. 4 April 2007. http://www.bafu.admin.ch/hydrologie/01835/02118/02120/index.html?lang=de. Retrieved 8 March 2008.
 |