Finance:Goodwin model (economics)

The Goodwin model, sometimes called Goodwin's class struggle model, is a model of endogenous economic fluctuations first proposed by the American economist Richard M. Goodwin in 1967. It combines aspects of the Harrod–Domar growth model with the Phillips curve to generate endogenous cycles in economic activity (output, unemployment and wages) unlike most modern macroeconomic models in which movements in economic aggregates are driven by exogenously assumed shocks. Since Goodwin's publication in 1967, the model has been extended and applied in various ways.

Model

The model is derived from the following assumptions:

1. there is steady growth of labour productivity (e.g. by technological improvement);
2. there is steady growth of the labour force (e.g. by births);
3. there are only two factors of production: labour and capital;
4. workers completely consume their wages, and capitalists completely invest their profits;
5. the capital-output ratio is constant (i.e. a fixed amount of output can always be turned into the same amount of capital);
6. real wages change according to a linearized Phillips curve, where wages rise when close to full employment.

The model uses the variables

q  is output

k  is (homogeneous) capital

w  is the wage rate

a  is labour productivity

n  is the labour force

which are all functions of time (although the time subscripts have been suppressed for convenience) and the constants

α  is the rate of growth of labour productivity

β  is the rate of growth of the labour force

γ  is used to define the real wage change curve

ρ  is also used to define the real wage change curve

σ  is the capital-output ratio.

A number of derived quantities are helpful to define the model. The amount of employed labour is given by

[math]\displaystyle{ l = \frac{q}{a} }[/math],

the employment ratio is given by

[math]\displaystyle{ v = \frac{l}{n} }[/math],

the workers' share in the output is given by

[math]\displaystyle{ u = \frac{w l}{q} = \frac{w}{a} }[/math],

and the share of the capitalists in the output ([math]\displaystyle{ s }[/math] for surplus) is given by

[math]\displaystyle{ s = 1 - u }[/math].

The model is then defined by a set of differential equations. Firstly, the change in labour productivity is defined by

[math]\displaystyle{ \frac{\dot{a}}{a} = \alpha }[/math],

that is, steady growth, with [math]\displaystyle{ a_t = a_0 e^{\alpha t} }[/math]. (Note that [math]\displaystyle{ \dot{x} }[/math] is the derivative over time [math]\displaystyle{ {dx}/{dt} }[/math].) The labour force changes according to

[math]\displaystyle{ \frac{\dot{n}}{n} = \beta }[/math],

again, steady growth, with [math]\displaystyle{ n_t = n_0 e^{\beta t} }[/math]. Real wages change according to

[math]\displaystyle{ \frac{\dot{w}}{w} = -\gamma + \rho v }[/math],

that is, the real wage change curve is modelled as linear. Note that to correctly model the assumptions, [math]\displaystyle{ \gamma }[/math] and [math]\displaystyle{ \rho }[/math] must be picked to ensure that real wages increase when [math]\displaystyle{ v }[/math] is near 1. In other words, if the labor market is 'tight' (employment is already high) there is upward pressure on wages and vice versa in a 'lax' labor market.

Capital changes according to

[math]\displaystyle{ \dot{k} = q s }[/math],

as the surplus is assumed to be completely invested by the capitalist. Lastly, output changes according to

[math]\displaystyle{ \frac{\dot{q}}{q} = \frac{s}{\sigma} }[/math],

that is, in proportion to the surplus invested.

Note that

[math]\displaystyle{ \frac{\dot{q}}{q} = \frac{\dot{k}}{k} = \frac{1 - u}{\sigma} }[/math]

by the assumption that k and q grow at the same rate by assumption of full utilization of capital and constant returns to scale.

Solution

The defining equations can be solved for [math]\displaystyle{ \dot{u} }[/math] and [math]\displaystyle{ \dot{v} }[/math], which gives the two differential equations

[math]\displaystyle{ \dot{v} = v(-\frac{1}{\sigma} u + \frac{1}{\sigma} - \alpha - \beta) }[/math]

[math]\displaystyle{ \dot{u} = u(\rho v - \gamma - \alpha) }[/math].

These are the key equations of the model and in fact are the Lotka–Volterra equations, which are used in biology to model predator-prey interaction. These equations have two fixed points. The first is when

[math]\displaystyle{ u = 0 }[/math] and [math]\displaystyle{ v = 0 }[/math]

and the second is when

[math]\displaystyle{ u = 1 - (\alpha + \beta)\sigma }[/math]

[math]\displaystyle{ v = \frac{\gamma + \alpha}{\rho} }[/math],

which determines the center of a family of cyclic trajectories.

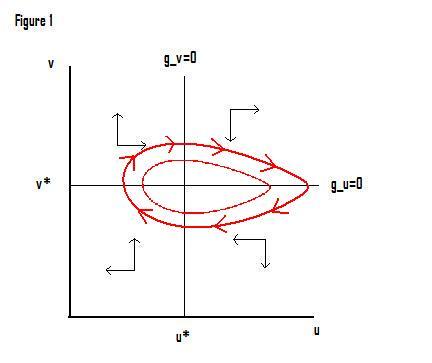
Since the model cannot be solved explicitly, it is instructive to analyze the trajectory of the economy in terms of a phase diagram. The two lines defining the center of the cycle divide the positive orthant into four regions. The figure below indicates with arrows the movement of the economy in each region. For example, the north-western region (high employment, low labor's share in output) the economy is moving north-east (employment is rising, worker's share is increasing). Once it crosses the u* line it will begin moving south-west.

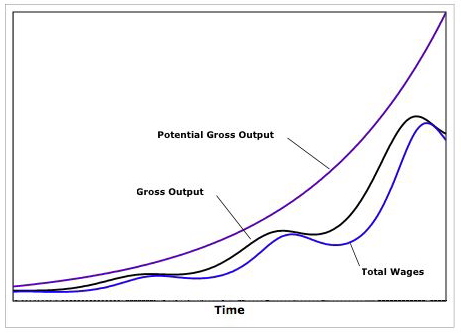
The figure below illustrates the movement of potential output (output at full employment), actual output and wages over time.

As can be seen the Goodwin model can generate endogenous fluctuations in economic activity without relying on extraneous assumptions of outside shocks, whether on the demand or supply side.

Statistics

• 

  Wage share (blue line) and civilian employment population ratio (red line) in the United States
  According to the Goodwin model, the wage share is to be expected to lag behind the employment rate. This seems to be the case if only by a small time lag

See also

• Business cycle
• Richard M. Goodwin
• Harrod–Domar model
• Marxian economics
• Phillips curve

References

• Goodwin, Richard M. (1967), "A Growth Cycle", in C.H. Feinstein, editor, Socialism, Capitalism and Economic Growth. Cambridge: Cambridge University Press.
• Goodwin, Richard M., Chaotic Economic Dynamics, Oxford University Press, 1990.
• Flaschel, Peter, The Macrodynamics of Capitalism - Elements for a Synthesis of Marx, Keynes and Schumpeter. Second edition, Springer Verlag Berlin 2010. Chapter 4.3.