Finance:Box spread

Profit diagram of a box spread. It is a combination of positions with a riskless payoff.

In options trading, a box spread is a combination of positions that has a certain (i.e., riskless) payoff, considered to be simply "delta neutral interest rate position". For example, a bull spread constructed from calls (e.g., long a 50 call, short a 60 call) combined with a bear spread constructed from puts (e.g., long a 60 put, short a 50 put) has a constant payoff of the difference in exercise prices (e.g. 10) assuming that the underlying stock does not go ex-dividend before the expiration of the options. If the underlying asset has a dividend of X, then the settled value of the box will be 10 + x. Under the no-arbitrage assumption, the net premium paid out to acquire this position should be equal to the present value of the payoff.

Box spreads' name derives from the fact that the prices for the underlying options form a rectangular box in two columns of a quotation. An alternate name is "alligator spread," derived from the large number of trades required to open and close them "eating" one's profit via commission fees.

Box spreads are usually only opened with European options, whose exercise is not allowed until the option's expiration. Most other styles of options, such as American, are less suitable, because they may expose traders to unwanted risk if one or more "legs" of a spread are exercised prematurely.

Background

An arbitrage operation may be represented as a sequence which begins with zero balance in an account, initiates transactions at time t = 0, and unwinds transactions at time t = T so that all that remains at the end is a balance whose value B will be known for certain at the beginning of the sequence. If there were no transaction costs then a non-zero value for B would allow an arbitrageur to profit by following the sequence either as it stands if the present value of B is positive, or with all transactions reversed if the present value of B is negative. However, market forces tend to close any arbitrage windows which might open; hence the present value of B is usually insufficiently different from zero for transaction costs to be covered. This is considered typically to be a "Market Maker/ Floor trader" strategy only, due to extreme commission costs of the multiple-leg spread. If the box is for example 20 dollars as per lower example getting short the box anything under 20 is profit and long anything over, has hedged all risk .

A present value of zero for B leads to a parity relation. Two well-known parity relations are:

• Spot futures parity: The current price of a stock equals the current price of a futures contract discounted by the time remaining until settlement:

[math]\displaystyle{ S = F e^{-rT} }[/math]

• Put call parity: A long European call c together with a short European put p at the same strike price K is equivalent to borrowing [math]\displaystyle{ K e^{-rT} }[/math] and buying the stock at price S. In other words, we can combine options with cash to construct a synthetic stock:

[math]\displaystyle{ c - p = S - K e^{-rT} }[/math]

Note that directly exploiting deviations from either of these two parity relations involves purchasing or selling the underlying stock.

The box spread

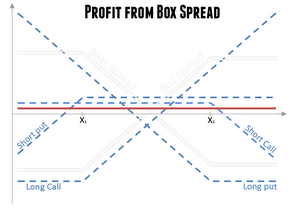
Now consider the put/call parity equation at two different strike prices [math]\displaystyle{ K_1 }[/math] and [math]\displaystyle{ K_2 }[/math]. The stock price S will disappear if we subtract one equation from the other, thus enabling one to exploit a violation of put/call parity without the need to invest in the underlying stock. The subtraction done one way corresponds to a long-box spread; done the other way it yields a short box-spread. The pay-off for the long box-spread will be the difference between the two strike prices, and the profit will be the amount by which the discounted payoff exceeds the net premium. For parity, the profit should be zero. Otherwise, there is a certain profit to be had by creating either a long box-spread if the profit is positive or a short box-spread if the profit is negative. [Normally, the discounted payoff would differ little from the net premium, and any nominal profit would be consumed by transaction costs.]

The long box-spread comprises four options, on the same underlying asset with the same terminal date. They can be paired in two ways as shown in the following table (assume strike-prices [math]\displaystyle{ K_1 }[/math] < [math]\displaystyle{ K_2 }[/math]):

	Long bull call-spread	Long bear put-spread
Long synthetic stock	Buy call at [math]\displaystyle{ K_1 }[/math]	Sell put at [math]\displaystyle{ K_1 }[/math]
Short synthetic stock	Sell call at [math]\displaystyle{ K_2 }[/math]	Buy put at [math]\displaystyle{ K_2 }[/math]

Reading the table horizontally and vertically, we obtain two views of a long box-spread.

• A long box-spread can be viewed as a long synthetic stock at a price [math]\displaystyle{ K_1 }[/math] plus a short synthetic stock at a higher price [math]\displaystyle{ K_2 }[/math].
• A long box-spread can be viewed as a long bull call spread at one pair of strike prices, [math]\displaystyle{ K_1 }[/math] and [math]\displaystyle{ K_2 }[/math], plus a long bear put spread at the same pair of strike prices.

We can obtain a third view of the long box-spread by reading the table diagonally. A long box-spread can be viewed as a long strangle at one pair of strike prices, [math]\displaystyle{ K_1 }[/math] and [math]\displaystyle{ K_2 }[/math], plus a short strangle at the same pair of strike prices.

• The long strangle contains the two long (buy) options.
• The short strangle contains the two short (sell) options.

A short box-spread can be treated similarly.

Example

As an example, consider a three-month option on a stock whose current price is $100. If the interest rate is 8% per annum and the volatility is 30% per annum, then the prices for the options might be:

	Call	Put
[math]\displaystyle{ K_1 = 90 }[/math]	$13.10	$ 1.65
[math]\displaystyle{ K_2 = 110 }[/math]	$3.05	$10.90

The initial investment for a long box-spread would be $19.30. The following table displays the payoffs of the 4 options for the three ranges of values for the terminal stock price [math]\displaystyle{ S_T }[/math]:

[math]\displaystyle{ S_T \lt K_1 }[/math]		[math]\displaystyle{ K_1 \lt S_T \lt K_2 }[/math]		[math]\displaystyle{ K_2 \lt S_T }[/math]
[math]\displaystyle{ 0 }[/math]	[math]\displaystyle{ S_T - 90 }[/math]	[math]\displaystyle{ S_T - 90 }[/math]	[math]\displaystyle{ 0 }[/math]	[math]\displaystyle{ S_T - 90 }[/math]	[math]\displaystyle{ 0 }[/math]
[math]\displaystyle{ 0 }[/math]	[math]\displaystyle{ 110 - S_T }[/math]	[math]\displaystyle{ 0 }[/math]	[math]\displaystyle{ 110 - S_T }[/math]	[math]\displaystyle{ 110 - S_T }[/math]	[math]\displaystyle{ 0 }[/math]

The terminal payoff has a value of $20 independent of the terminal value of the share price. The discounted value of the payoff is $19.60. Hence there is a nominal profit of 30 cents to be had by investing in the long box-spread.

Prevalence

Surveys done by Chaput and Ederington on the Chicago Mercantile Exchange's market for options on Eurodollar futures showed that between 1999 and 2000, some 25% of the trading volume was in outright options, 25% in straddles and vertical spreads (call-spreads and put-spreads), and about 5% in strangles. Guts constituted only about 0.1%, and box-spreads even less (about 0.01%). Ratio spreads took more than 15%, and about a dozen other instruments took the remaining 30%.

Diamond and van Tassel found that the difference between the implied "risk free" rate through box spreads and Treasuries, or similar investments in other countries' central banks, is a "convenience yield" for the ease of investment in the central bank's securities. This convenience yield is between 10 and 60 basis points for ten major countries and is approximately 35 basis points for Treasuries, the most widely held government security. The difference between box spreads and government securities will tend to increase when there is financial instability, increase as interest rates rise, and increase for shorter maturities.

Robinhood incident

In January 2019, a member of the Reddit community /r/WallStreetBets realized a loss of more than $57,000 on $5,000 principal by attempting a box spread through Robinhood, which provides commission-free options trading. The user, who initially asserted that "[the spread] literally cannot go tits up," did not realize that the American options he was using carried the risk of being exercised, and had his spread liquidated entirely when this happened to one of its legs. (He had been exposed to as much as $212,500 in risk with the spread open.) Robinhood subsequently announced that investors on the platform would no longer be able to open box spreads, a policy that remains in place as of October 2022.

See also

• Jelly roll (options)

Further reading

• Uri, Benzion; Shmuel, Danan; Joseph, Yagil (Spring 2005). "Box Spread Strategies and Arbitrage Opportunities". The Journal of Derivatives 12 (3): 47–62. doi:10.3905/jod.2005.479379. 
• Bharadwaj, Anu; Wiggins, James B. (2001). "Box spread and put-call parity tests for the S&P 500 index LEAPS market". The Journal of Derivatives 8 (4): 62–71. doi:10.3905/jod.2001.319163.  The box-spread reveals an arbitrage profit insufficient to cover transaction costs.
• Billingsley, R.S.; Chance, Don M. (1987). "Options market efficiency and the box spread strategy". Financial Review 20 (4): 287–301. doi:10.1111/j.1540-6288.1985.tb00309.x. 
• Chance, Don M. (2001). An Introduction to Derivatives (5th ed.). Thomson. 
• Template:Cite SSRN
• Hemler, Michael L.; Miller, Thomas W. Jr. (1997). "Box spread arbitrage profits following the 1987 market crash: real or illusory?". Journal of Financial and Quantitative Analysis 32 (1): 71–90. doi:10.2307/2331317. . Post-market simulations with box-spreads on the S&P 500 Index show that market ineffiency increased after the 1987 crash.
• Hull, John C. (2002). Fundamentals of Futures and Options Markets (4th ed.). Prentice-Hall. 
• Ronn, Edud; Gerbarg Ronn, Aimee (1989). "The Box spread arbitrage conditions: theory, tests, and investment strategies". Review of Financial Studies 2 (1): 91–108. doi:10.1093/rfs/2.1.91.  The box-spread is used to test for arbitrage opportunities on Chicago Board Options Exchange data.