np-chart

np-chart
Originally proposed by	Walter A. Shewhart
Process observations
Rational subgroup size	n > 1
Measurement type	Number nonconforming per unit
Quality characteristic type	Attributes data
Underlying distribution	Binomial distribution
Performance
Size of shift to detect	≥ 1.5σ
Process variation chart
Not applicable
Process mean chart
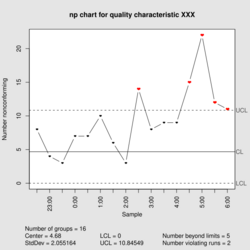Center line	[math]\displaystyle{ n \bar p = \frac {\sum_{i=1}^m \sum_{j=1}^n \begin{cases} 1 & \mbox{if }x_{ij}\mbox{ defective} \\ 0 & \mbox{otherwise} \end{cases}}{m} }[/math]
Control limits	[math]\displaystyle{ n \bar p \pm 3\sqrt{n \bar p(1- \bar p)} }[/math]
Plotted statistic	[math]\displaystyle{ n \bar p_i = \sum_{j=1}^n \begin{cases} 1 & \mbox{if }x_{ij}\mbox{ defective} \\ 0 & \mbox{otherwise} \end{cases} }[/math]

In statistical quality control, the np-chart is a type of control chart used to monitor the number of nonconforming units in a sample. It is an adaptation of the p-chart and used in situations where personnel find it easier to interpret process performance in terms of concrete numbers of units rather than the somewhat more abstract proportion.

The np-chart differs from the p-chart in only the three following aspects:

1. The control limits are [math]\displaystyle{ n\bar p \pm 3\sqrt{n\bar p(1-\bar p)} }[/math], where n is the sample size and [math]\displaystyle{ \bar p }[/math] is the estimate of the long-term process mean established during control-chart setup.
2. The number nonconforming (np), rather than the fraction nonconforming (p), is plotted against the control limits.
3. The sample size, [math]\displaystyle{ n }[/math], is constant.

See also

• p-chart