Chemistry:Thermodynamics of micellization
In colloidal chemistry, the critical micelle concentration (CMC) of a surfactant is one of the parameters in the Gibbs free energy of micellization. The concentration at which the monomeric surfactants self-assemble into thermodynamically stable aggregates is the CMC. The Krafft temperature of a surfactant is the lowest temperature required for micellization to take place. There are many parameters that affect the CMC. The interaction between the hydrophilic heads and the hydrophobic tails play a part, as well as the concentration of salt within the solution and surfactants.
Micelle
A micelle is an aggregation of surfactants or block copolymer in aqueous solution or organic solution, often spherical.
Surfactants
Surfactants are composed of a polar head group that is hydrophilic and a nonpolar tail group that is hydrophobic. The head groups can be anionic, cationic, zwitterionic, or nonionic. The tail group can be a hydrocarbon, fluorocarbon, or a siloxane. Extensive variation in the surfactant’s solution and interfacial properties is allowed through different molecular structures of surfactants.[1]
Hydrophobic coagulation occurs when a positively charged solution is added with a sodium alkyl sulfate. The coagulation value is smaller when the alkyl chain length of the coagulator is longer. Hydrophobic coagulation occurs when a negatively charged solution contains a cationic surfactant. The coulomb attraction between the head groups and surface competes with the hydrophobic attraction for the entire tail in a favorable manner.[1]
Block copolymer
Block copolymers are interesting because they can "microphase separate" to form periodic nanostructures,[13][14][15] Microphase separation is a situation similar to that of oil and water. Oil and water are immiscible - they phase separate. Due to incompatibility between the blocks, block copolymers undergo a similar phase separation. Because the blocks are covalently bonded to each other, they cannot demix macroscopically as water and oil. In "microphase separation" the blocks form nanometer-sized structures.
Driving mechanism for micellization
The driving mechanism for micellization is the transfer of hydrocarbon chains from water into the oil-like interior. This entropic effect is called the hydrophobic effect. Compared to the increase of entropy of the surrounding water molecules, this hydrophobic interaction is relatively small. The water molecules are highly ordered around the hydrocarbon chain. The CMC decreases while the length of the alkyl chain increases when all the hydrocarbon chains are hidden inside micelles.[2]
Ionic micelles and salt concentration
The driving force for adsorption is the attraction between the surface and the surfactant head-group with low surfactant concentrations and the adsorption on hydrophilic surfaces. This means that the surfactant adsorbs at low surfactant concentrations with its head-group contacting the surface. Depending on the type of head-group and surface, the attraction will have a short-range contribution for both non-ionic and ionic surfactants. Ionic surfactants will also experience a generic electrostatic interaction. If the surfactants and the surface are oppositely charged then the interaction will be attractive.[2][page needed] If the surfactants and the surface are like charges then the interaction will be repulsive.[2] Aggregation is opposed due to the repulsion of the polar head groups as they come closer to each other. Hydration repulsion occurs because head groups have to be dehydrated as they come closer to each other.[2] The head groups’ thermal fluctuations become smaller as they come closer together because they are confined by neighboring head groups.[2] This causes their entropy to decrease and leads to a repulsion.[2]
Gibbs free energy of micellization
In general, the Gibbs free energy of micellization can be approximated as:
[math]\displaystyle{ \Delta G_{micellization} = - RT \times \ln (CMC) }[/math][1]
where [math]\displaystyle{ \Delta G_{micellization} }[/math] is the change in Gibbs free energy of micellization, [math]\displaystyle{ R }[/math] is the universal gas constant, [math]\displaystyle{ T }[/math] is the absolute temperature, and [math]\displaystyle{ CMC }[/math] is the critical micelle concentration.
Non-ionic micelles
Two methods to extract the Gibbs free energy based on the value of CMC and [math]\displaystyle{ n }[/math] exist; Phillips method[3] based on the law of mass action and the pseudo-phase separation model. The law of mass action postulates that the micelle formation can be modeled as a chemical equilibrium process between the micelles [math]\displaystyle{ M_n }[/math] and its constituents, the surfactant monomers, [math]\displaystyle{ S }[/math]:
[math]\displaystyle{ n \cdot S \rightleftharpoons M_n }[/math],
where [math]\displaystyle{ n }[/math] is the average number of surfactant monomers in solution that associate into a micelle, commonly denoted the aggregation number.
The equilibrium is characterized by an equilibrium constant defined by [math]\displaystyle{ K=[M_n]/[S]^n }[/math], where [math]\displaystyle{ [M_n] }[/math] and [math]\displaystyle{ [S] }[/math] are the concentrations of micelles and free surfactant monomers, respectively. In combination with the law of conservation of mass, the system is fully specified by: [math]\displaystyle{ S_{tot}=[S]+nK[S]^n }[/math], where [math]\displaystyle{ S_{tot} }[/math] is the total surfactant concentration. Phillips[3] defined the CMC as the point corresponding to the maximum change in gradient in an ideal property-concentration ([math]\displaystyle{ \phi }[/math] against [math]\displaystyle{ S_{tot} }[/math]) relationship [math]\displaystyle{ \frac{d^3\phi}{dS^3_{tot}} }[/math]=0. By implicit differentiation of [math]\displaystyle{ S_{tot}=[S]+nK[S]^n }[/math] three times with respect to [math]\displaystyle{ S_{tot} }[/math] and equating to zero it can be shown[4] that the micellization constant is given by [math]\displaystyle{ K=\frac{n-2}{n^2(2n-1)}\left(CMC \cdot \frac{2n^2-n}{2n^2-2} \right)^{1-n} }[/math] for [math]\displaystyle{ n\gt 2 }[/math]. According to Phillips method the Gibbs free energy change of micellization is therefore given by:
[math]\displaystyle{ \Delta G_{micellization}=-\frac{RT}{n}\ln \left(\frac{n-2}{n^2(2n-1)}\left(CMC \cdot \frac{2n^2-n}{2n^2-2} \right)^{1-n}\right) }[/math]
The pseudo-phase separation model was originally derived on its own basis, but it has later been shown that it can be interpreted as an approximation to the mass-action model for large [math]\displaystyle{ n }[/math]. That is, for micelles behaving in accordance with the law of mass-action, the pseudo-phase phase separation model is only an approximation and will only become asymptotically equal to the mass-action model as the micelle becomes a true macroscopic phase i.e. for [math]\displaystyle{ n }[/math]→∞. However, the approximation that the aggregation number [math]\displaystyle{ n }[/math] is large is in most cases sufficient:
[math]\displaystyle{ \Delta G_{micellization} \approx RT\ln (CMC) }[/math]
Ionic micelles
Ionic micelles are typically very affected by the salt concentration. In ionic micelles the monomers are typically fully ionized, but the high electric field strength at the surface of the micelles will cause adsorption of some proportion of the free counter-ions. In this case a chemical equilibrium process can be assumed between the charged micelles [math]\displaystyle{ M_n^{-(1-\beta)n} }[/math] and its constituents, the bile salt monomers, [math]\displaystyle{ S^- }[/math] and bound counter-ions [math]\displaystyle{ B^+ }[/math]:
[math]\displaystyle{ n \cdot S^- + \beta\cdot n \cdot B^+ \rightleftharpoons M_n^{-(1-\beta)n} }[/math]
where [math]\displaystyle{ n }[/math] is the average aggregation number and [math]\displaystyle{ \beta }[/math] is the average degree of counter-ion binding to the micelle. In this case, the Gibbs free energy is given by:[4]
[math]\displaystyle{ \Delta G_{micellization}=-\frac{RT}{n}\ln \left(\frac{1}{\left([B^+]_{S_{tot}=CMC}\right)^{\beta n}}\frac{n-2}{n^2(2n-1)}\left(CMC \cdot \frac{2n^2-n}{2n^2-2} \right)^{1-n}\right) }[/math]
where [math]\displaystyle{ \Delta G_{micellization} }[/math] is the Gibbs energy of micellization and [math]\displaystyle{ [B^+]_{S_{tot}=CMC} }[/math] is the free counter-ion concentration at CMC. For large [math]\displaystyle{ n }[/math], that is in the limit when then the micelles becomes a true macroscopic phase, the Gibbs free energy is usually approximated by:
[math]\displaystyle{ \Delta G_{micellization}\approx (1+\beta)RT\ln CMC }[/math]
Dressed micelle model
In the dressed micelle model, the total Gibbs energy is broken down into several components accounting for the hydrophobic tail, the electrostatic repulsion of the head groups, and the interfacial energy on the surface of the micelle.
[math]\displaystyle{ \Delta G_{micellization}=\Delta G_{HP} +\Delta G_{EL} +\Delta G_{IF} }[/math][5]
where the components of the total Gibbs micellization energy are hydrophobic, electrostatic, and interfacial.
Effect of concentration and temperature
Solubility and cloud point
Specific temperature at a specific pressure at which large groups of micelles begin to precipitate out into a quasi-separate phase.[6] As temperature is raised above the cloud point this causes the distinct surfactant phase to form densely packed micelle groups known as aggregates.[6] The phase separation is a reversible separation controlled by enthalpy (promotes aggregation/separation) above the cloud point, and entropy (promotes miscibility of micelles in water) below the cloud point. The cloud point is the equilibrium between the two free energies.[6]
Critical micelle concentration
The critical micelle concentration (CMC) is the exact concentration of surfactants at which aggregates become thermodynamically soluble in an aqueous solution. Below the CMC there is not a high enough density of surfactant to spontaneously precipitate into a distinct phase.[7] Above the CMC, the solubility of the surfactant within the aqueous solution has been exceeded. The energy required to keep the surfactant in solution no longer is the lowest energy state. To decrease free energy of the system the surfactant is precipitated out. CMC is determined by establishing inflection points for pre-determined surface tension of surfactants in solution. Plotting the inflection point against the surfactant concentration will provide insight into the critical micelle concentration by showing stabilization of phases.[7]
Krafft temperature
The Krafft temperature is the temperature at which the CMC can be achieved. This temperature determines the relative solubility of surfactant in an aqueous solution. This is the minimum temperature the solution must be at to allow the surfactant to precipitate into aggregates.[8] Below this temperature no level of solubility will be sufficient to precipitate aggregates due to minimal movement of particles in solution.[8] The Krafft Temperature (Tk) is based on the concentration of counter-ions (Caq).[8] Counter-ions are typically in the form of salt. Because the Tk is fundamentally based on the Caq, which is controlled by surfactant and salt concentration, different combinations of the respective parameters can be altered.[8] Although, the Caq will maintain the same value despite changes in concentration of surfactant and salt, therefore, thermodynamically speaking the Krafft temperature will remain constant.[8]
Surfactant packing parameter
Differences in shape
The shape of a surfactant molecule can be described by its surfactant packing parameter, [math]\displaystyle{ N_{\text{S}} }[/math] (Israelachvili, 1976).[9] The packing parameter takes into account the volume of the hydrophobic chain ([math]\displaystyle{ V_c }[/math]), the equilibrium area per molecule at the aggregate interface ([math]\displaystyle{ a_e }[/math]), and the length of the hydrophobic chain ([math]\displaystyle{ L_c }[/math]):[10]
[math]\displaystyle{ N_{\text{S}} = \frac { V_c } {a_e * L_c} }[/math][1] The packing parameter for a specific surfactant is not a constant. It is dependent on various conditions which affect each the volume of the hydrophobic chain, the cross sectional area of the hydrophilic head group, and the length of the hydrophobic chain. Things that can affect these include, but are not limited to, the properties of the solvent, the solvent temperature, and the ionic strength of the solvent.
Cone, wedge, and cylinder shaped surfactants
The shape of a micelle is directly dependent on the packing parameter of the surfactant. Surfactants with a packing parameter of [math]\displaystyle{ N_{\text{S}} }[/math] ≤ 1/3 appear to have a cone-like shape which will pack together to form spherical micelles when in an aqueous environment (top in figure).[10][11] Surfactants with a packing parameter of 1/3 < [math]\displaystyle{ N_{\text{S}} }[/math] ≤ 1/2 appear to have a wedge-like shape and will aggregate together in an aqueous environment to form cylindrical micelles (bottom in figure).[10][11] Surfactants with a packing parameter of [math]\displaystyle{ N_{\text{S}} }[/math] > 1/2 appear to have a cylindrical shape and pack together to form a bilayer in an aqueous environment (middle in figure).[10][11]
Data
| Surfactant | Structure | CMC (mM) | ΔG°[math]\displaystyle{ _{micellization} }[/math] (kJ/mol) |
|---|---|---|---|
| Sodium dodecyl sulfate (SDS) | 8.2[12] | -22.00 | |
| Sodium octyl sulfate (SOS) | 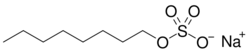
|
-- | -14.71 |
| Cetyl trimethylammonium bromide (CTAB) | 0.89−0.93[13] | -30.46[14] |
References
- ↑ 1.0 1.1 1.2 1.3 Butt, Graf, Kappl (March 10, 2006). Physics and Chemistry of Interfaces. Weinheim: Wiley-VCH. pp. 269–277. ISBN 9783527406296. OCLC 1127799271. https://books.google.com/books?id=gTNHAQAAIAAJ.
- ↑ 2.0 2.1 2.2 2.3 2.4 2.5 Esumi, Kunio; Ueno, Minoru (August 15, 1997). Structure-Performance Relationships In Surfactants. Taylor & Francis. ISBN 9780824700683. OCLC 37201301. https://books.google.com/books?id=KhFtAAAAMAAJ.
- ↑ 3.0 3.1 J.N. Phillips. Trans. Faraday Soc. 51 (1955) 561-569
- ↑ 4.0 4.1 N.E. Olesen. Journal of Colloid and Interface Science. 453 (2015) 79-89
- ↑ Stokes, Evans (1997). Fundamentals of Interfacial Engineering. New York: Wiley and Sons. pp. 222. ISBN 978-0-471-18647-2.
- ↑ 6.0 6.1 6.2 Paleologos, Evangelos K.; Giokas, Dimosthenis L.; Karayannis, Miltiades I. (2005). "Micelle-mediated separation and cloud-point extraction". Trends in Analytical Chemistry 24 (5): 426–436. doi:10.1016/j.trac.2005.01.013.
- ↑ 7.0 7.1 Daniel E. Klle, Cary 1. Chlou, Water Solubility Enhancements of DDT and Trichlorobenzene by Some Surfactants Below and Above the Critical Micelle Concentration, Environ. Sci Technol. 1989, 23, 832-838
- ↑ 8.0 8.1 8.2 8.3 8.4 Carolina Vautier-Giongo, Barney L. Bales, Estimate of the Ionization Degree of Ionic Micelles Based on Krafft Temperature Measurements, J. Phys. Chem. B 2003, 107, 5398-5403
- ↑ Israelachvili, Jacob N. (1976). "Theory of self-assembly of hydrocarbon amphiphiles into micelles and bilayers". Journal of the Chemical Society, Faraday Transactions 2: Molecular and Chemical Physics 72: 1525–1568. doi:10.1039/f29767201525.
- ↑ 10.0 10.1 10.2 10.3 Cullis, Pieter (1986). "Lipid Polymorphism and the Roles of Lipids in Membranes". Chemistry and Physics of Lipids 40 (2–4): 127–144. doi:10.1016/0009-3084(86)90067-8. PMID 3742670.
- ↑ 11.0 11.1 11.2 Borsali, Pecora (2008). Soft-Matter Characterization. Springer. pp. 195. ISBN 978-1402044649.
- ↑ P. Mukerjee and K. J. Mysels, "Critical Micelle Concentration of Aqueous Surfactant Systems", NSRDS-NBS 36, US. Government Printing Office, Washington, D.C., 197 1.
- ↑ Wang, Yaofeng (2009). "Encapsulation of Myoglobin in a Cetyl Trimethylammonium Bromide Micelle in Vacuo: A Simulation Study". Biochemistry 48 (5): 1006–1015. doi:10.1021/bi801952f. PMID 19154126.
- ↑ Rodriguez, Amalia (2003). "Water-Ethylene Glycol Alkyltrimethylammonium Bromide Micellar Solutions as Reaction Media: Study of Spontaneous Hydrolysis of Phenyl Chloroformate". Langmuir 19 (18): 7206–7213. doi:10.1021/la0301137.
 |



