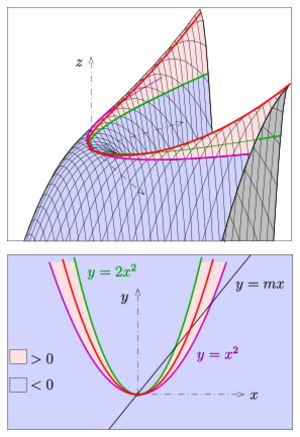
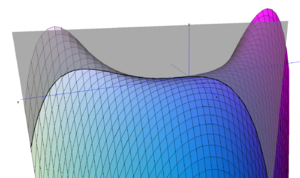
Peano surface
In mathematics, the Peano surface is the graph of the two-variable function
- [math]\displaystyle{ f(x,y)=(2x^2-y)(y-x^2). }[/math]
It was proposed by Giuseppe Peano in 1899 as a counterexample to a conjectured criterion for the existence of maxima and minima of functions of two variables.[1][2]
The surface was named the Peano surface (German: Peanosche Fläche) by Georg Scheffers in his 1920 book Lehrbuch der darstellenden Geometrie.[1][3] It has also been called the Peano saddle.[4][5]
Properties
The function [math]\displaystyle{ f(x,y)=(2x^2-y)(y-x^2) }[/math] whose graph is the surface takes positive values between the two parabolas [math]\displaystyle{ y=x^2 }[/math] and [math]\displaystyle{ y=2x^2 }[/math], and negative values elsewhere (see diagram). At the origin, the three-dimensional point [math]\displaystyle{ (0,0,0) }[/math] on the surface that corresponds to the intersection point of the two parabolas, the surface has a saddle point.[6] The surface itself has positive Gaussian curvature in some parts and negative curvature in others, separated by another parabola,[4][5] implying that its Gauss map has a Whitney cusp.[5]
Although the surface does not have a local maximum at the origin, its intersection with any vertical plane through the origin (a plane with equation [math]\displaystyle{ y=mx }[/math] or [math]\displaystyle{ x=0 }[/math]) is a curve that has a local maximum at the origin,[1] a property described by Earle Raymond Hedrick as "paradoxical".[7] In other words, if a point starts at the origin [math]\displaystyle{ (0,0) }[/math] of the plane, and moves away from the origin along any straight line, the value of [math]\displaystyle{ (2x^2-y)(y-x^2) }[/math] will decrease at the start of the motion. Nevertheless, [math]\displaystyle{ (0,0) }[/math] is not a local maximum of the function, because moving along a parabola such as [math]\displaystyle{ y=\sqrt{2}\,x^2 }[/math] (in diagram: red) will cause the function value to increase.
The Peano surface is a quartic surface.
As a counterexample
In 1886 Joseph Alfred Serret published a textbook[8] with a proposed criteria for the extremal points of a surface given by [math]\displaystyle{ z=f(x_0+h,y_0+k) }[/math]
- "the maximum or the minimum takes place when for the values of [math]\displaystyle{ h }[/math] and [math]\displaystyle{ k }[/math] for which [math]\displaystyle{ d^2f }[/math] and [math]\displaystyle{ d^3f }[/math] (third and fourth terms) vanish, [math]\displaystyle{ d^4f }[/math] (fifth term) has constantly the sign − , or the sign +."
Here, it is assumed that the linear terms vanish and the Taylor series of [math]\displaystyle{ f }[/math] has the form [math]\displaystyle{ z=f(x_0,y_0)+Q(h,k)+C(h,k)+F(h,k)+\cdots }[/math] where [math]\displaystyle{ Q(h,k) }[/math] is a quadratic form like [math]\displaystyle{ a h^2+b h k+c k^2 }[/math], [math]\displaystyle{ C(h,k) }[/math] is a cubic form with cubic terms in [math]\displaystyle{ h }[/math] and [math]\displaystyle{ k }[/math], and [math]\displaystyle{ F(h,k) }[/math] is a quartic form with a homogeneous quartic polynomial in [math]\displaystyle{ h }[/math] and [math]\displaystyle{ k }[/math]. Serret proposes that if [math]\displaystyle{ F(h,k) }[/math] has constant sign for all points where [math]\displaystyle{ Q(h,k)=C(h,k)=0 }[/math] then there is a local maximum or minimum of the surface at [math]\displaystyle{ (x_0,y_0) }[/math].
In his 1884 notes to Angelo Genocchi's Italian textbook on calculus, Calcolo differenziale e principii di calcolo integrale, Peano had already provided different correct conditions for a function to attain a local minimum or local maximum.[1][9] In the 1899 German translation of the same textbook, he provided this surface as a counterexample to Serret's condition. At the point [math]\displaystyle{ (0,0,0) }[/math], Serret's conditions are met, but this point is a saddle point, not a local maximum.[1][2] A related condition to Serret's was also criticized by Ludwig Scheeffer, who used Peano's surface as a counterexample to it in an 1890 publication, credited to Peano.[6][10]
Models
Models of Peano's surface are included in the Göttingen Collection of Mathematical Models and Instruments at the University of Göttingen,[11] and in the mathematical model collection of TU Dresden (in two different models).[12] The Göttingen model was the first new model added to the collection after World War I, and one of the last added to the collection overall.[6]
References
- ↑ 1.0 1.1 1.2 1.3 1.4 Emch, Arnold (1922). "A model for the Peano Surface". American Mathematical Monthly 29 (10): 388–391. doi:10.1080/00029890.1922.11986180. https://archive.org/details/jstor-2299024.
- ↑ 2.0 2.1 Genocchi, Angelo (1899). Peano, Giuseppe. ed (in German). Differentialrechnung und Grundzüge der Integralrechnung. B.G. Teubner. p. 332. https://archive.org/details/differentialrec01genogoog/page/n348.
- ↑ Scheffers, Georg (1920). "427. Die Peanosche Fläche" (in German). Lehrbuch der darstellenden Geometrie. II. pp. 261–263. https://archive.org/details/lehrbuchderdarst02sche/page/260.
- ↑ 4.0 4.1 Krivoshapko, S. N.; Ivanov, V. N. (2015). "Saddle Surfaces". Encyclopedia of Analytical Surfaces. Springer. pp. 561–565. doi:10.1007/978-3-319-11773-7_33. See especially section "Peano Saddle", pp. 562–563.
- ↑ 5.0 5.1 5.2 Francis, George K. (1987). A Topological Picturebook. Springer-Verlag, New York. p. 88. ISBN 0-387-96426-6.
- ↑ 6.0 6.1 6.2 Fischer, Gerd, ed (2017). Mathematical Models: From the Collections of Universities and Museums – Photograph Volume and Commentary (2nd ed.). doi:10.1007/978-3-658-18865-8. ISBN 978-3-658-18864-1. See in particular the Foreword (p. xiii) for the history of the Göttingen model, Photo 122 "Penosche Fläsche / Peano Surface" (p. 119), and Chapter 7, Functions, Jürgen Leiterer (R. B. Burckel, trans.), section 1.2, "The Peano Surface (Photo 122)", pp. 202–203, for a review of its mathematics.
- ↑ Hedrick, E. R. (July 1907). "A peculiar example in minima of surfaces". Annals of Mathematics. Second Series 8 (4): 172–174. doi:10.2307/1967821.
- ↑ Serret, J. A. (1886). Cours de calcul différentiel et intégral. 1 (3d ed.). Paris. p. 216. https://archive.org/details/coursdecalculdif01serruoft/page/216/mode/2up.
- ↑ Genocchi, Angelo (1884). "Massimi e minimi delle funzioni di più variabili". in Peano, Giuseppe (in Italian). Calcolo differenziale e principii di calcolo integrale. Fratelli Bocca. pp. 195–203. https://archive.org/details/calcolodifferen00peangoog/page/n234.
- ↑ Scheeffer, Ludwig (December 1890). "Theorie der Maxima und Minima einer Function von zwei Variabeln" (in German). Mathematische Annalen 35 (4): 541–576. doi:10.1007/bf02122660. https://eudml.org/doc/157480. See in particular pp. 545–546.
- ↑ "Peano Surface". Göttingen Collection of Mathematical Models and Instruments. University of Göttingen. http://modellsammlung.uni-goettingen.de/index.php?r=7&sr=32&m=443&lang=en. Retrieved 2020-07-13.
- ↑ Model 39, "Peanosche Fläche, geschichtet" and model 40, "Peanosche Fläche", Mathematische Modelle, TU Dresden, retrieved 2020-07-13
External links
 |