Fast Walsh–Hadamard transform
In computational mathematics, the Hadamard ordered fast Walsh–Hadamard transform (FWHTh) is an efficient algorithm to compute the Walsh–Hadamard transform (WHT). A naive implementation of the WHT of order [math]\displaystyle{ n = 2^m }[/math] would have a computational complexity of O([math]\displaystyle{ n^2 }[/math]). The FWHTh requires only [math]\displaystyle{ n \log n }[/math] additions or subtractions.
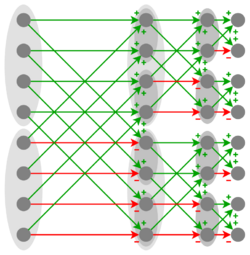
The FWHTh is a divide-and-conquer algorithm that recursively breaks down a WHT of size [math]\displaystyle{ n }[/math] into two smaller WHTs of size [math]\displaystyle{ n/2 }[/math]. [1] This implementation follows the recursive definition of the [math]\displaystyle{ 2^m \times 2^m }[/math] Hadamard matrix [math]\displaystyle{ H_m }[/math]:
- [math]\displaystyle{ H_m = \frac{1}{\sqrt 2} \begin{pmatrix} H_{m-1} & H_{m-1} \\ H_{m-1} & -H_{m-1} \end{pmatrix}. }[/math]
The [math]\displaystyle{ 1/\sqrt2 }[/math] normalization factors for each stage may be grouped together or even omitted.
The sequency-ordered, also known as Walsh-ordered, fast Walsh–Hadamard transform, FWHTw, is obtained by computing the FWHTh as above, and then rearranging the outputs.
A simple fast nonrecursive implementation of the Walsh–Hadamard transform follows from decomposition of the Hadamard transform matrix as [math]\displaystyle{ H_m = A^m }[/math], where A is m-th root of [math]\displaystyle{ H_m }[/math]. [2]
Python example code
def fwht(a) -> None:
"""In-place Fast Walsh–Hadamard Transform of array a."""
h = 1
while h < len(a):
# perform FWHT
for i in range(0, len(a), h * 2):
for j in range(i, i + h):
x = a[j]
y = a[j + h]
a[j] = x + y
a[j + h] = x - y
# normalize and increment
a /= math.sqrt(2)
h *= 2
See also
References
- ↑ Fino, B. J.; Algazi, V. R. (1976). "Unified Matrix Treatment of the Fast Walsh–Hadamard Transform". IEEE Transactions on Computers 25 (11): 1142–1146. doi:10.1109/TC.1976.1674569.
- ↑ Yarlagadda and Hershey, "Hadamard Matrix Analysis and Synthesis", 1997 (Springer)
External links
- Charles Constantine Gumas, A century old, the fast Hadamard transform proves useful in digital communications
 |