Antiparallel (mathematics)

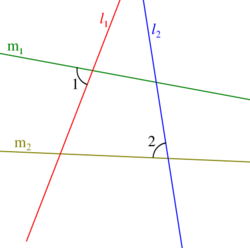
In geometry, two lines [math]\displaystyle{ l_1 }[/math] and [math]\displaystyle{ l_2 }[/math] are antiparallel with respect to a given line [math]\displaystyle{ m }[/math] if they each make congruent angles with [math]\displaystyle{ m }[/math] in opposite senses. More generally, lines [math]\displaystyle{ l_1 }[/math] and [math]\displaystyle{ l_2 }[/math] are antiparallel with respect to another pair of lines [math]\displaystyle{ m_1 }[/math] and [math]\displaystyle{ m_2 }[/math] if they are antiparallel with respect to the angle bisector of [math]\displaystyle{ m_1 }[/math] and [math]\displaystyle{ m_2. }[/math]

In any cyclic quadrilateral, any two opposite sides are antiparallel with respect to the other two sides.

Lines [math]\displaystyle{ l_1 }[/math] and [math]\displaystyle{ l_2 }[/math] are antiparallel with respect to the line [math]\displaystyle{ m }[/math] if they make the same angle with [math]\displaystyle{ m }[/math] in the opposite senses.	Two lines [math]\displaystyle{ l_1 }[/math] and [math]\displaystyle{ l_2 }[/math] are antiparallel with respect to the sides of an angle if they make the same angle [math]\displaystyle{ \angle APC }[/math] in the opposite senses with the bisector of that angle.
Given two lines [math]\displaystyle{ m_1 }[/math] and [math]\displaystyle{ m_2 }[/math], lines [math]\displaystyle{ l_1 }[/math] and [math]\displaystyle{ l_2 }[/math] are antiparallel with respect to [math]\displaystyle{ m_1 }[/math] and [math]\displaystyle{ m_2 }[/math] if [math]\displaystyle{ \angle 1 = \angle 2 }[/math].	In any quadrilateral inscribed in a circle, any two opposite sides are antiparallel with respect to the other two sides.

Relations

1. The line joining the feet to two altitudes of a triangle is antiparallel to the third side. (any cevians which 'see' the third side with the same angle create antiparallel lines)
2. The tangent to a triangle's circumcircle at a vertex is antiparallel to the opposite side.
3. The radius of the circumcircle at a vertex is perpendicular to all lines antiparallel to the opposite sides.

References

• A.B. Ivanov, Encyclopaedia of Mathematics - ISBN:1-4020-0609-8
• Weisstein, Eric W. "Antiparallel." From MathWorld—A Wolfram Web Resource. [1]