Baumslag–Solitar group

One sheet of the Cayley graph of the Baumslag–Solitar group BS(1, 2). Red edges correspond to a and blue edges correspond to b.

The sheets of the Cayley graph of the Baumslag-Solitar group BS(1, 2) fit together into an infinite binary tree.

Visualization comparing the sheet and the binary tree Cayley graph of [math]\displaystyle{ \text{BS}(1,2) }[/math]. Red and blue edges correspond to [math]\displaystyle{ a }[/math] and [math]\displaystyle{ b }[/math], respectively.

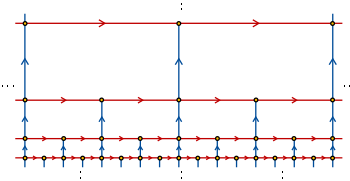
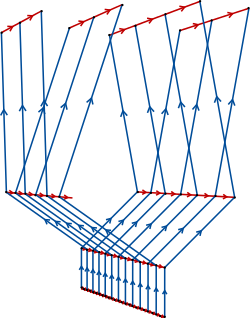
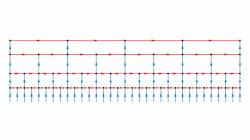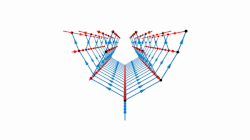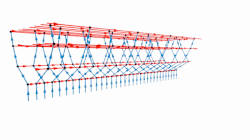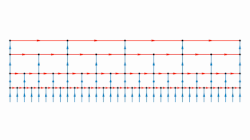
In the mathematical field of group theory, the Baumslag–Solitar groups are examples of two-generator one-relator groups that play an important role in combinatorial group theory and geometric group theory as (counter)examples and test-cases. They are given by the group presentation

[math]\displaystyle{ \left \langle a, b \ : \ b a^m b^{-1} = a^n \right \rangle. }[/math]

For each integer m and n, the Baumslag–Solitar group is denoted BS(m, n). The relation in the presentation is called the Baumslag–Solitar relation.

Some of the various BS(m, n) are well-known groups. BS(1, 1) is the free abelian group on two generators, and BS(1, −1) is the fundamental group of the Klein bottle.

The groups were defined by Gilbert Baumslag and Donald Solitar in 1962 to provide examples of non-Hopfian groups. The groups contain residually finite groups, Hopfian groups that are not residually finite, and non-Hopfian groups.

Linear representation

Define

[math]\displaystyle{ A= \begin{pmatrix}1&1\\0&1\end{pmatrix}, \qquad B= \begin{pmatrix}\frac{n}{m}&0\\0&1\end{pmatrix}. }[/math]

The matrix group G generated by A and B is a homomorphic image of BS(m, n), via the homomorphism induced by

[math]\displaystyle{ a\mapsto A, \qquad b\mapsto B. }[/math]

It is worth noting that this will not, in general, be an isomorphism. For instance if BS(m, n) is not residually finite (i.e. if it is not the case that |m| = 1, |n| = 1, or |m| = |n|) it cannot be isomorphic to a finitely generated linear group, which is known to be residually finite by a theorem of Anatoly Maltsev.

See also

• Binary tiling
• Solv geometry

References

• Hazewinkel, Michiel, ed. (2001), "Baumslag–Solitar group", Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=B/b130070 
• Gilbert Baumslag and Donald Solitar, Some two-generator one-relator non-Hopfian groups, Bulletin of the American Mathematical Society 68 (1962), 199–201. MR0142635