Multinomial theorem
In mathematics, the multinomial theorem describes how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem from binomials to multinomials.
Theorem
For any positive integer m and any non-negative integer n, the multinomial formula describes how a sum with m terms expands when raised to an arbitrary power n:
- [math]\displaystyle{ (x_1 + x_2 + \cdots + x_m)^n = \sum_{k_1+k_2+\cdots+k_m=n; \ k_1, k_2, \cdots, k_m \geq 0} {n \choose k_1, k_2, \ldots, k_m} \prod_{t=1}^m x_t^{k_t}\,, }[/math]
where
- [math]\displaystyle{ {n \choose k_1, k_2, \ldots, k_m} = \frac{n!}{k_1!\, k_2! \cdots k_m!} }[/math]
is a multinomial coefficient. The sum is taken over all combinations of nonnegative integer indices k1 through km such that the sum of all ki is n. That is, for each term in the expansion, the exponents of the xi must add up to n. Also, as with the binomial theorem, quantities of the form x0 that appear are taken to equal 1 (even when x equals zero).
In the case m = 2, this statement reduces to that of the binomial theorem.
Example
The third power of the trinomial a + b + c is given by
- [math]\displaystyle{ (a+b+c)^3 = a^3 + b^3 + c^3 + 3 a^2 b + 3 a^2 c + 3 b^2 a + 3 b^2 c + 3 c^2 a + 3 c^2 b + 6 a b c. }[/math]
This can be computed by hand using the distributive property of multiplication over addition, but it can also be done (perhaps more easily) with the multinomial theorem. It is possible to "read off" the multinomial coefficients from the terms by using the multinomial coefficient formula. For example:
- [math]\displaystyle{ a^2 b^0 c^1 }[/math] has the coefficient [math]\displaystyle{ {3 \choose 2, 0, 1} = \frac{3!}{2!\cdot 0!\cdot 1!} = \frac{6}{2 \cdot 1 \cdot 1} = 3. }[/math]
- [math]\displaystyle{ a^1 b^1 c^1 }[/math] has the coefficient [math]\displaystyle{ {3 \choose 1, 1, 1} = \frac{3!}{1!\cdot 1!\cdot 1!} = \frac{6}{1 \cdot 1 \cdot 1} = 6. }[/math]
Alternate expression
The statement of the theorem can be written concisely using multiindices:
- [math]\displaystyle{ (x_1+\cdots+x_m)^n = \sum_{|\alpha|=n}{n \choose \alpha}x^\alpha }[/math]
where
- [math]\displaystyle{ \alpha=(\alpha_1,\alpha_2,\dots,\alpha_m) }[/math]
and
- [math]\displaystyle{ x^\alpha=x_1^{\alpha_1} x_2^{\alpha_2} \cdots x_m^{\alpha_m} }[/math]
Proof
This proof of the multinomial theorem uses the binomial theorem and induction on m.
First, for m = 1, both sides equal x1n since there is only one term k1 = n in the sum. For the induction step, suppose the multinomial theorem holds for m. Then
- [math]\displaystyle{ \begin{align} & (x_1+x_2+\cdots+x_m+x_{m+1})^n = (x_1+x_2+\cdots+(x_m+x_{m+1}))^n \\[6pt] = {} & \sum_{k_1+k_2+\cdots+k_{m-1}+K=n}{n\choose k_1,k_2,\ldots,k_{m-1},K} x_1^{k_1} x_2^{k_2}\cdots x_{m-1}^{k_{m-1}}(x_m+x_{m+1})^K \end{align} }[/math]
by the induction hypothesis. Applying the binomial theorem to the last factor,
- [math]\displaystyle{ = \sum_{k_1+k_2+\cdots+k_{m-1}+K=n}{n\choose k_1,k_2,\ldots,k_{m-1},K} x_1^{k_1}x_2^{k_2}\cdots x_{m-1}^{k_{m-1}}\sum_{k_m+k_{m+1}=K}{K\choose k_m,k_{m+1}}x_m^{k_m}x_{m+1}^{k_{m+1}} }[/math]
- [math]\displaystyle{ = \sum_{k_1+k_2+\cdots+k_{m-1}+k_m+k_{m+1}=n}{n\choose k_1,k_2,\ldots,k_{m-1},k_m,k_{m+1}} x_1^{k_1}x_2^{k_2}\cdots x_{m-1}^{k_{m-1}}x_m^{k_m}x_{m+1}^{k_{m+1}} }[/math]
which completes the induction. The last step follows because
- [math]\displaystyle{ {n\choose k_1,k_2,\ldots,k_{m-1},K}{K\choose k_m,k_{m+1}} = {n\choose k_1,k_2,\ldots,k_{m-1},k_m,k_{m+1}}, }[/math]
as can easily be seen by writing the three coefficients using factorials as follows:
- [math]\displaystyle{ \frac{n!}{k_1! k_2! \cdots k_{m-1}!K!} \frac{K!}{k_m! k_{m+1}!}=\frac{n!}{k_1! k_2! \cdots k_{m+1}!}. }[/math]
Multinomial coefficients
The numbers
- [math]\displaystyle{ {n \choose k_1, k_2, \ldots, k_m} }[/math]
appearing in the theorem are the multinomial coefficients. They can be expressed in numerous ways, including as a product of binomial coefficients or of factorials:
- [math]\displaystyle{ {n \choose k_1, k_2, \ldots, k_m} = \frac{n!}{k_1!\, k_2! \cdots k_m!} = {k_1\choose k_1}{k_1+k_2\choose k_2}\cdots{k_1+k_2+\cdots+k_m\choose k_m} }[/math]
Sum of all multinomial coefficients
The substitution of xi = 1 for all i into the multinomial theorem
- [math]\displaystyle{ \sum_{k_1+k_2+\cdots+k_m=n} {n \choose k_1, k_2, \ldots, k_m} x_1^{k_1} x_2^{k_2} \cdots x_m^{k_m} = (x_1 + x_2 + \cdots + x_m)^n }[/math]
gives immediately that
- [math]\displaystyle{ \sum_{k_1+k_2+\cdots+k_m=n} {n \choose k_1, k_2, \ldots, k_m} = m^n. }[/math]
Number of multinomial coefficients
The number of terms in a multinomial sum, #n,m, is equal to the number of monomials of degree n on the variables x1, …, xm:
- [math]\displaystyle{ \#_{n,m} = {n+m-1 \choose m-1}. }[/math]
The count can be performed easily using the method of stars and bars.
Valuation of multinomial coefficients
The largest power of a prime p that divides a multinomial coefficient may be computed using a generalization of Kummer's theorem.
Asymptotics
By Stirling's approximation, or equivalently the log-gamma function's asymptotic expansion, [math]\displaystyle{ \log\binom{kn}{n, n, \cdots, n} = k n \log(k) + \frac{1}{2} \left(\log(k) - (k - 1) \log(2 \pi n)\right) - \frac{k^2 - 1}{12kn} + \frac{k^4 - 1}{360k^3n^3} - \frac{k^6 - 1}{1260k^5n^5} + O\left(\frac{1}{n^6}\right) }[/math]so for example,[math]\displaystyle{ \binom{2n}{n} \sim \frac{2^{2n}}{\sqrt{n\pi }} }[/math]
Interpretations
Ways to put objects into bins
The multinomial coefficients have a direct combinatorial interpretation, as the number of ways of depositing n distinct objects into m distinct bins, with k1 objects in the first bin, k2 objects in the second bin, and so on.[1]
Number of ways to select according to a distribution
In statistical mechanics and combinatorics, if one has a number distribution of labels, then the multinomial coefficients naturally arise from the binomial coefficients. Given a number distribution {ni} on a set of N total items, ni represents the number of items to be given the label i. (In statistical mechanics i is the label of the energy state.)
The number of arrangements is found by
- Choosing n1 of the total N to be labeled 1. This can be done [math]\displaystyle{ \tbinom{N}{n_1} }[/math] ways.
- From the remaining N − n1 items choose n2 to label 2. This can be done [math]\displaystyle{ \tbinom{N-n_1}{n_2} }[/math] ways.
- From the remaining N − n1 − n2 items choose n3 to label 3. Again, this can be done [math]\displaystyle{ \tbinom{N-n_1-n_2}{n_3} }[/math] ways.
Multiplying the number of choices at each step results in:
- [math]\displaystyle{ {N \choose n_1}{N-n_1\choose n_2}{N-n_1-n_2\choose n_3}\cdots=\frac{N!}{(N-n_1)!n_1!} \cdot \frac{(N-n_1)!}{(N-n_1-n_2)!n_2!} \cdot \frac{(N-n_1-n_2)!}{(N-n_1-n_2-n_3)!n_3!}\cdots. }[/math]
Cancellation results in the formula given above.
Number of unique permutations of words
The multinomial coefficient
- [math]\displaystyle{ \binom{n}{k_1, \ldots, k_m} }[/math]
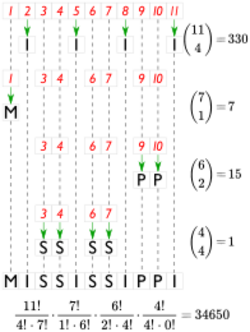
is also the number of distinct ways to permute a multiset of n elements, where ki is the multiplicity of each of the ith element. For example, the number of distinct permutations of the letters of the word MISSISSIPPI, which has 1 M, 4 Is, 4 Ss, and 2 Ps, is
- [math]\displaystyle{ {11 \choose 1, 4, 4, 2} = \frac{11!}{1!\, 4!\, 4!\, 2!} = 34650. }[/math]
Generalized Pascal's triangle
One can use the multinomial theorem to generalize Pascal's triangle or Pascal's pyramid to Pascal's simplex. This provides a quick way to generate a lookup table for multinomial coefficients.
See also
References
- ↑ National Institute of Standards and Technology (May 11, 2010). "NIST Digital Library of Mathematical Functions". Section 26.4. http://dlmf.nist.gov/. Retrieved August 30, 2010.
 |